Time & Distance Questions for RRB Group-D Set-2 PDF
Download Top-15 RRB Group-D Time & Distance Questions set-2 PDF. RRB GROUP-D Maths questions based on asked questions in previous exam papers very important for the Railway Group-D exam.
Download Time & Distance Questions for RRB Group-D Set-2 PDF
Download RRB Group-D Previous Papers PDF
Take a RRB Group-D free mock test
Question 1: Walking at a speed of 10 km/hr, Madhu reaches her university 15 minutes late. Next time she increases her speed by 2 km/hr, but she is still late by 5 minutes. The distance of the university from her house is:
a) 15 km
b) 30 km
c) 20 km
d) 10 km
Question 2: Driving @ 48 $\frac{km}{hr}$ Barun reached the destination 2 minutes ahead of time. If he drove @ 42 $\frac{km}{hr}$ he would have been 1 minute late. What is the distance that Barun drove?
a) 17.6 km
b) 17.2 km
c) 16.4 km
d) 16.8 km
Question 3: Rahim started a journey 15 minutes late, and as a result, had to drive at a speed of 54 km/h instead of 45 km/h to reach his destination on time. What is the distance covered during the course of the journey?
a) 90 km
b) 67.5 km
c) 13.5 km
d) 75.5 km
Take a free mock test for RRB Group-D
770 Mocks (cracku Pass) Just Rs.199
Question 4: A car starting from rest, accelerates in a straight road at a constant rate of 3.0 $ms^{-2}$ for 8 s. Find the distance travelled by the car during this time.
a) 75 m
b) 86 m
c) 96 m
d) 100 m
Question 5: A car starts from city A and travels towards city B at a speed of 60 kmph. After one hour, a bike starts from city B and travels towards city A at a speed of 40 kmph. After the bike and the car cross each other, the time taken by the car to reach city B is 4 hours less than the time taken by the bike to reach city A. What is the distance between the 2 cities (in km)?
Question 6: Raman and Rajeev leave their respective houses at the speed of 6 kmph and 4 kmph respectively to meet at a common point lying somewhere in the middle. Raman has a horse who is very excited about the meeting. He leaves Raman’s house, at the same time, and goes towards Rajeev, and after meeting him, comes back to Raman and then again goes to Rajeev. In this way, the horse continues his to and fro journey at the speed of 15 kmph till the three of them meet. If the total distance covered by the horse is $3k$ km, what is the distance between the houses of Raman and Rajeev (in km)?
a) $k$
b) $2k$
c) $3k$
d) $5k$
Question 7: A and B are at a distance of 1.7 km apart and they start running towards each other at a speed of 8 m/s and 9 m/s respectively. Afier how much time, will they meet each other?
a) 1 minute 4 seconds
b) 14 seconds
c) 14 minutes
d) 1 minute 40 seconds
RRB Group D previous year papers
Question 8: A girl walks to school from her house at 5 km/h speed for 24 minutes and cycles back the same distance at 8 km/h. The time taken to cycle back is:
a) 15 minutes
b) 8 minutes
c) 10 minutes
d) 21 minutes
Question 9: The distance between two cities is covered in $3\frac{1}{4}$ hours at a speed of 52 km/h. If the speed is increased to 65 km/h. how much time would be saved ?
a) 39 minutes
b) 45 minutes
c) 40 minutes
d) 42 minutes
Question 10: A train needs to travel 400 km. It travels half of the distance at 160 km/hr and remaining half of the distance at 120 km/hr. In how much time it can travel total distance?
a) 180 min
b) 175 min
c) 160 min
d) 150 min
Question 11: Two players A and B runs from a same point with their speeds in the ratio 3:4$\pi$. A runs to and fro diagonally while B runs along the circumference. If the radius is 2m find the total distance traveled by A by the time they will meet again?
a) 24m
b) 12m
c) 48m
d) 36m
RRB Group-D Important Questions (download PDF)
Question 12: Raj takes $2\dfrac{1}{3}$ hours to complete a certain distance at a speed of 51 km/hr. What time would Kiran take to complete the same distance at a speed of 68km/hr?
a) $1\frac{2}{3}$ hours
b) $1\frac{3}{4}$ hours
c) $2$ hours
d) $1\frac{1}{2}$ hours
Question 13: The distance between two places can be covered in 3 $\frac{1}{2}$ hours at a speed of 62 km/hr.If the speed is increased by 8 km/hr, how much time would be saved?
a) 20 minutes
b) 24 minutes
c) 15 minutes
d) 30 minutes
Question 14: 37 trees are planted in a straight line such that distance between any two consecutive trees is same. A car takes 20 seconds to reach the 13th tree. How much more time (in seconds) will it take to reach the last tree?
a) 36
b) 40
c) 57
d) 60
Question 15: Two boats P and Q run between two cities A and B on a stream with flow of 5 km/h. The cities are 300 km apart and P and Q have still water speeds of 25 km/h and 15 km/h respectively. P and Q start from cities A and B towards B and A respectively at the same time. When and where will they meet for the second time?
a) After 20 hours at 100 km from B
b) After 10 hours at 100 km from B
c) After 12 hours at 100 km from B
d) After 20 hours at 200 km from B
General Science Notes for RRB Exams (PDF)
Answers & Solutions:
1) Answer (D)
2) Answer (D)
3) Answer (B)
4) Answer (C)
5) Answer: 360
Let the distance between the 2 cities be ‘x’ km.
By the time the bike starts, the car has already traveled for an hour (60 km).
Distance between the car and the bike when the bike starts = (x-60) km.
Time taken by the car and bike to meet each other after the bike starts = (x-60)/(40+60) = (x-60)/100 hours.
The car takes 4 hours less to reach city B than the time taken by the bike to reach city A.
Let ‘t’ be the time taken by the car to reach city B after crossing the bike.
=> t*60 = (x-60)/100 * 40
t = (x-60)/150 ———(1)
Time taken by the bike after crossing the car to reach city A = t+4 hours.
(t +4)*40 = (x-60)/100*60 + 60
t+4 = 1.5(x+40)/100
t+4 = (1.5x + 60)/100
t = (1.5x-340)/100 ————(2)
Equating (1) and (2), we get,
(x-60)/150 = (1.5x-340)/100
2x – 120 = 4.5x – 1020
2.5x = 900
x = 360 km
6) Answer (B)
The horse will keep running at the speed of 15 kmph until Raman and Rajeev meet.
Let us assume the distance between their houses is $x$ km.
Since both are moving towards each other,
their relative speed = (6 + 4) kmph = 10 kmph
So, time required to meet = $\dfrac{x}{10}$ hr
Distance covered by the horse = $3k$ km
Time taken by the horse = $\dfrac{3k}{15}$ hr
Both the times must be equal.
So, $\dfrac{x}{10}$ = $\dfrac{3k}{15}$
On solving, we get
$x = 2k$
Hence, option B is the correct answer.
7) Answer (D)
8) Answer (A)
9) Answer (A)
10) Answer (B)
Given that the train travels first 200 km at 160 km/hr
Time taken = $\dfrac{200}{160} = \dfrac{5}{4}$ hours
Train travels remaining 200 km at 120 km/hr
Time taken = $\dfrac{200}{120} = \dfrac{5}{3}$ hours
Total time taken = $\dfrac{5}{4} + \dfrac{5}{3} = \dfrac{15 + 20}{12} = \dfrac{35}{12} \times 60 = 175$ minutes
11) Answer (A)
Ratio of the speed of A and B = 3:4$\pi$. This implies that for every 3m traveled by A , B will travel 4$\pi$m.
Radius of the Circle =2m
Circumference of the circle =4$\pi$m.
Hence for one complete round of B, A will travel 3m.
A cannot meet B at a diametrically opposite point because for every meter A moves B covers a one-third of a circle.
Thus they will meet at the same point.
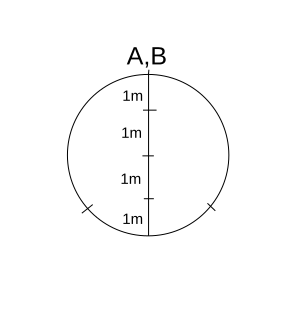
For A to reach back at the starting point it will travel 8m.
Thus for both the players to reach at the same point it has to be a multiple of 3 and 8 which is 24.
Hence the answer is Option A.
12) Answer (B)
Speed of Raj = 51 km/hr
Time taken by Raj to travel a certain distance = $2\dfrac{1}{3} = \dfrac{7}{3}$ hours
Hence, Distance travelled by Raj = $\dfrac{7}{3} \times 51 = 119 km$
Given, Speed of Kiran = 68 km/hr
Time required for Kiran to travel 119 km at 68 km/hr = $\dfrac{119}{68} = \dfrac{7}{4} = 1\dfrac{3}{4}$ hours
13) Answer (B)
14) Answer (B)
Let the distance between any two consecutive trees = $d$ metres
=> Total distance between the 37 trees = $36d$ metres
Time taken to reach the 13th tree = 20 seconds
=> Speed of car = distance/time
= $\frac{12d}{20}=\frac{3d}{5}$ m/s
Thus, time taken to reach the last tree from the first tree = $\frac{36d}{\frac{3d}{5}}$
= $36\times\frac{5}{3}=60$ seconds
$\therefore$ The car will take (60-20) = 40 seconds more to reach the last tree
=> Ans – (B)
15) Answer (D)
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Time & Distance Questions set-2 PDF for RRB Group-D Exam will be highly useful for your preparation.





