Syllogisms are verbal reasoning type questions. This topic holds a significant weightage in all banking exams. Once we are well aware of the concept, syllogism problems are easier to solve. Hence, understanding its basic concept is very crucial.
For IBPS exam read Syllogism questions and answers for IBPS PO
In this blog, we will discuss 7 tips to solve syllogism questions for SBI PO.
Unlimited Banking Tests – Rs. 499
Contents
SYLLOGISMS FOR SBI PO
Syllogism questions for SBI PO are logical argument type of questions, which require the application of deductive reasoning to arrive at a conclusion. The typical question format of this type of questions is, two or more premises or statements followed by a set of conclusions will be given. And, you need to find which conclusion logically follows the given assumptions.
One important thing you need to remember while solving syllogism questions is that consider the given assumptions or statements to be true even if they don’t agree with commonly known facts.
The best method to solve syllogisms is through Venn-diagrams. Though it seems to be a time-consuming method, practicing syllogisms through Venn-diagrams eliminates a lot of confusion while solving them in the actual exam. Practice syllogism questions in Previous Papers of SBI PO to ace this section in this years SBI PO exam.
7 TIPS TO SOLVE SYLLOGISM QUESTIONS FOR SBI PO.
1) Derivable conclusions from the statement “All P are Q”.
The Venn-diagram for the statement is a bigger circle representing Q encircling a smaller circle representing P. The diagram is as shown below.
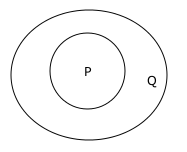
The conclusions that can be derived from the given statement are
* Some P are Q
* Some Q are P
Also, there is a possibility that the below diagram represents the given statement.
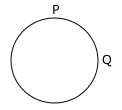
But, this is the more limiting case. We cannot use this second diagram unless more information is available. The pro-tip one must remember while drawing Venn-diagrams is, always draw the less limiting case. i.e., in this case, one must always use the first diagram unless any further information was given.
2) Derivable conclusions from the statement “No A is B”.
The Venn-diagram for this statement is two non-intersecting circles representing A and B. The Venn-diagram for this statement is as shown below.
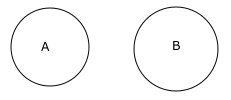
Conclusions derivable:
* No B is A
* Some A are not B
* Some B are not A
This statement says that overlap between A and B does not exist. This doesn’t mean A and B cannot overlap another set.
Download SBI Po 2018 Syllabus PDF
3) Derivable conclusions from the statement “Some M are N”.
The Venn-diagram for this statement can be drawn in four ways. In each of the below diagrams, Statement ‘some M are N’ holds true. Hence, we cannot decide which of the following diagrams must be used to draw conclusions, without having any further information.
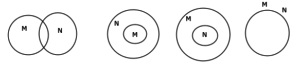
The conclusion that can be definitely derived from the given statement, without using further information is
*Some N are M
Remember the statement “Some M are N” doesn’t necessarily mean “Some M are not N”.
4) Derivable conclusions from the statement “Some A are not B”.
This statement is somewhat similar to the above-discussed case. The Venn-diagram for this statement can be drawn in three ways. In each of the below diagrams, statement ‘some A are not B’ holds true.
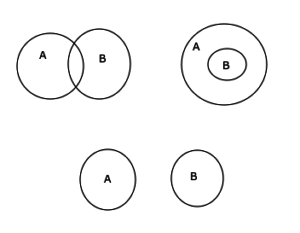
There are no definite conclusions that can be derived from the statement, but the statement eliminates the case “All A are B”.
5) Derivable conclusions from the statement “Some J are K. All K are T”.
The Venn-diagram for this statement can be drawn in many ways; one of the possible ways is as shown below.
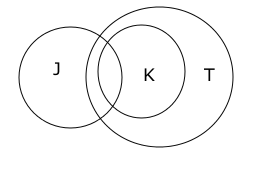
Conclusions derivable:
* Some T are J
* Few T are K
* Some K are J
* Few J are T
6) Complementary pairs:
A complementary pair of conclusions is a pair which is mutually exclusive and exhaustive, each conclusion being the complement of the other conclusion.
‘Either conclusion 1 or conclusion 2’ case can only be seen in complementary pairs.
For example, take two random sets D and B.
Conclusion 1 : Some D are not B Conclusion 2: All D are B
It is evident that, among the above-mentioned conclusions, one of the conclusions must be true. ‘Either 1 or 2’ option must be selected in this case. So, this is an example of a complementary pair.
7) Possibility cases:
Sometimes, syllogism questions come with possibility conclusions. That is, the question asks if the given conclusion is possible or not. In order to solve such problems, we have to consider all the possible Venn-diagrams.
For example, consider the following example.
Statement: Some A are B.
Conclusion: All A are B is a possibility
As we have discussed in point 2, there exist four possible Venn-diagrams for the given statement. And one of them is all A being B. Therefore, the given conclusion is true.
So, one should keep all the above-mentioned tips to solve syllogism questions for SBI PO. in mind while solving syllogisms for SBI PO exam. Now that we have learned the concept, let take a look at the following examples.
Daily Current Affairs – Today current Affairs PDF
EXAMPLES:
Example 1:
Statements:
1) All men are women
2) All women are kids
Conclusions:
1) Some kids are men
2) All men are kids
The less limiting Venn-diagram for the above-mentioned statements would be as shown below.
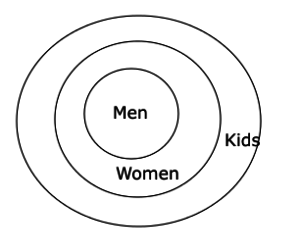
All men are women + All women are kids ==> All men are kids. —> Conclusion 2 is true.
The statement ‘All men are kids’ implies ‘some kids are men’ —> Conclusion 1 is true.
Therefore, both the conclusions follow.
Example 2:
Statements:
1) Some birds are animals
2) Some animals are fishes
Conclusions:
1) No bird is a fish
2) No bird is a fish is a possibility
Below drawn Venn-diagrams are two out of many possibilities.
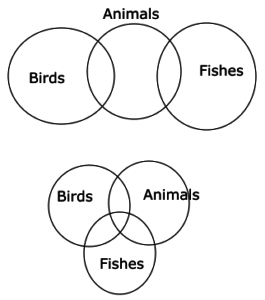
No bird being fish is a possible scenario. But, this is not a necessary scenario. So, only conclusion 2 is correct.
Download SBI PO Free Preparation App
Therefore, the correct option to choose is only conclusion 2 follows.
So, these are the 7 tips to solve syllogism questions for SBI PO. These can also be helpful for all other banking exams.





![How To Manage Time In CAT Exam? [Section-wise Tips] How to manage time in CAT exam ?](https://cracku.in/blog/wp-content/uploads/2018/09/fig-03-09-2018_10-54-46-218x150.jpg)
provide 1 speed test free to look before 1 buy test series for sbi po 2017