Geometry Quadrilaterals Question for SSC CHSl and MTS

Here you can download SSC CHSL & MTS 2022 – important SSC CHSL & MTS Geometry Quadrilaterals Questions PDF by Cracku. Very Important SSC CHSL & MTS 2022 and These questions will help your SSC CHSL & MTS preparation. So kindly download the PDF for reference and do more practice.

Download Geometry Quadrilaterals Question for SSC CHSl and MTS

Enroll to 15 SSC CHSL 2022 Mocks At Just Rs. 149

Question 1: Vertices A, B, C and D of a quadrilateral ABCD lie on a circle. $\angle$A is three times $\angle$C and $\angle$D is two times $\angle$B. What is the difference between the measures of $\angle$D and $\angle$C?

a) $55^\circ$

b) $65^\circ$

c) $75^\circ$

d) $45^\circ$

1) Answer (C)

Solution:

Given,

$\angle$A is three times $\angle$C and $\angle$D is two times $\angle$B.

$\angle$A = 3$\angle$C…….(1)

$\angle$D = 2$\angle$B…….(2)

In a cyclic quadrilateral, opposite angles are supplementary.

$\angle$A + $\angle$C = 180$^\circ$ and $\angle$B + $\angle$D = 180$^\circ$

$\angle$A + $\angle$C = 180$^\circ$

3$\angle$C + $\angle$C = 180$^\circ$  [From (1)]

4$\angle$C = 180$^\circ$

$\angle$C = 45$^\circ$

$\angle$A = 3$\angle$C = 135$^\circ$

$\angle$B + $\angle$D = 180$^\circ$

$\angle$B + 2$\angle$B = 180$^\circ$  [From (2)]

3$\angle$B = 180$^\circ$

$\angle$B = 60$^\circ$

$\angle$D = 2$\angle$B = 120$^\circ$

Difference between the measures of $\angle$D and $\angle$C = 120$^\circ$ – 45$^\circ$

= 75$^\circ$

Hence, the correct answer is Option C

Question 2: ABCD is a cyclic quadrilateral such that when sides AB and DC are produced, they meet at E, and sides AD and BC meet at F, when produced. If $\angle$ADE = 80$^\circ$ and $\angle$AED = 50$^\circ$, then what is the measure of $\angle$AFB?

a) $40^\circ$

b) $20^\circ$

c) $50^\circ$

d) $30^\circ$

2) Answer (D)

Solution:

From triangle AED,

$\angle$ADE + $\angle$AED + $\angle$DAE = 180$^\circ$

80$^\circ$ + 50$^\circ$ + $\angle$DAE = 180$^\circ$

$\angle$DAE = 50$^\circ$

ABCD is a cyclic quadrilateral.

Opposite angles in a cyclic quadrilateral is supplementary.

$\angle$ADC + $\angle$ABC = 180$^\circ$

80$^\circ$ + $\angle$ABC = 180$^\circ$

$\angle$ABC = 100$^\circ$

From triangle ABF,

$\angle$ABF + $\angle$AFB + $\angle$BAF = 180$^\circ$

100$^\circ$ + $\angle$AFB + 50$^\circ$ = 180$^\circ$

$\angle$AFB = 30$^\circ$

Hence, the correct answer is Option D

Question 3: ABCD is cyclic quadrilateral in which $\angle$A = x$^\circ$, $\angle$B = 5y$^\circ$, $\angle$C = 2x$^\circ$ and $\angle$D = y$^\circ$. What is the value of (3x – y)?

a) 120

b) 90

c) 150

d) 60

3) Answer (C)

Solution:

ABCD is cyclic quadrilateral.

Opposite angles in a cyclic quadrilateral are supplementary.

$\angle$A + $\angle$C = 180$^\circ$

x + 2x = 180$^\circ$

3x = 180$^\circ$

x = 60$^\circ$

$\angle$B + $\angle$D = 180$^\circ$

5y + y = 180$^\circ$

6y = 180$^\circ$

y = 30$^\circ$

3x – y = 3(60) – 30 = 150

Hence, the correct answer is Option C

Question 4: Triangle ABC is an equilateral triangle. D and E are points on AB and AC respectively such that DE is parallel to BC and is equal to half the length of BC. If AD + CE + BC = 30 cm, then find the perimeter (in cm) of the quadrilateral BCED.

a) 37.5

b) 25

c) 45

d) 35

4) Answer (A)

Solution:

Triangle ABC is an equilateral triangle.

Let the length of BC = 2p

BC = AB = AC = 2p

DE is equal to half the length of BC.

Triangle ABC and triangle ADE are similar triangles.

$\Rightarrow$  $\frac{AD}{AB}=\frac{DE}{BC}$

$\Rightarrow$  $\frac{AD}{AB}=\frac{p}{2p}$

$\Rightarrow$  $AD=\frac{1}{2}AB$

$\Rightarrow$  $AD=\frac{1}{2}\times2p$

$\Rightarrow$  AD = p

Similarly, AE = p

and EC = AC – AE = 2p – p = p

AD + CE + BC = 30 cm

p + p + 2p = 30

4p = 30

p = $\frac{15}{2}$ cm

Perimeter of the quadrilateral BCED = BD + DE + CE + BC

= p + p + p + 2p

= 5p

= $5\times\frac{15}{2}$

= 37.5 cm

Hence, the correct answer is Option A

Question 5: In the figure, a circle touches all the four sides of a quadrilateral ABCD whose sides AB = 6.5 cm, BC = 5.4 cm and CD = 5.3 cm. The length of AD is:

a) 4.6 cm

b) 5.8 cm

c) 6.2 cm

d) 6.4 cm

5) Answer (D)

Solution:

Given, AB = 6.5 cm, BC = 5.4 cm and CD = 5.3 cm

Let the circle touches AB, BC, CD, DA at T, R, Q, S respectively.

Length of tangents to the circle from an external point are equal.

AT = AS

BT = BR

CQ = CR

DQ = DS

Adding all of the above

AT + BT + CQ + DQ = AS + BR + CR + DS

$\Rightarrow$  (AT + BT) + (CQ + DQ) = (AS + DS) + (BR + CR)

$\Rightarrow$  AB + CD = AD + BC

$\Rightarrow$  6.5 + 5.3 = AD + 5.4

$\Rightarrow$  AD = 6.4 cm

Hence, the correct answer is Option D

Take a free SSC CHSL Tier-1 mock test

Download SSC CGL Tier-1 Previous Papers PDF

Question 6: The three medians AX, BY and CZ of $\triangle$ABC intersect at point L. If the area of $\triangle$ABC is 30 $cm^2$, then the area of the quadrilateral BXLZ is:

a) 10 $cm^2$

b) 12 $cm^2$

c) 16 $cm^2$

d) 14 $cm^2$

6) Answer (A)

Solution:

Given, Area of $\triangle$ABC = 30 $cm^2$

The three medians AX, BY and CZ of $\triangle$ABC intersect at point L as shown in the above figure

The area of six triangles in the above figure are equal and area is equal to one-sixth of the area of triangle ABC.

Area of $\triangle$BLX = $\frac{1}{6}\times$Area of $\triangle$ABC

= $\frac{1}{6}\times$30

= 5 $cm^2$

Similarly, Area of $\triangle$BLZ = 5 $cm^2$

$\therefore\ $Area of quadrilateral = Area of $\triangle$BLX + Area of $\triangle$BLZ = 5 + 5 = 10 $cm^2$

Hence, the correct answer is Option A

Question 7: In the given figure, PQRS is a cyclic quadrilateral. What is the measure of the angle PQR if PQ is parallel to SR?

a) $110^\circ$

b) $80^\circ$

c) $100^\circ$

d) $70^\circ$

7) Answer (A)

Solution:

In the cyclic quadrilateral PQRS,

Sum of opposite angles = 180$^{\circ\ }$

$=$>  $\angle$SPQ + $\angle$SRQ = 180$^{\circ\ }$

$=$>  110$^{\circ\ }$ + $\angle$SRQ = 180$^{\circ\ }$

$=$>  $\angle$SRQ = 70$^{\circ\ }$

Given, PQ is parallel to SR

RQ is the transversal intersecting the parallel lines PQ and SR

Sum of the interior angles on the same side of the transversal is 180$^{\circ\ }$

$=$>  $\angle$SRQ + $\angle$PQR = 180$^{\circ\ }$

$=$>  70$^{\circ\ }$ + $\angle$PQR = 180$^{\circ\ }$

$=$>  $\angle$PQR = 110$^{\circ\ }$

Hence, the correct answer is Option A

Question 8: ABCD is a cyclic quadrilateral which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If $\angle A = 60^\circ$ and $\angle ABC = 72^\circ$, then \angle PDC – $\angle DPC =$

a) $24^\circ$

b) $30^\circ$

c) $36^\circ$

d) $40^\circ$

8) Answer (A)

Solution:

In $\triangle ABP$,

$\angle A + \angle ABC + \angle APB = 180\degree$

$\angle APB = 180 – 60 – 72 = 48\degree $

$\angle ADC = 180 – ABC = 180 – 72 = 108\degree$
$\angle PDC = 180 – \angle ADC = 180 – 108 = 72\degree$

$\angle PDC – \angle DPC = 72 – 48 = 24\degree$

Question 9: In quadrilateral PQRS, RM $\perp$ QS, PN $\perp$ QS and QS = 6 cm. If RM = 3 cm and PN = 2 cm, then the area of PQRS is

a) 13 $cm^2$

b) 15 $cm^2$

c) 14 $cm^2$

d) 11 $cm^2$

9) Answer (B)

Solution:

Area of PQRS = area of $\triangle$PQS + area of $\triangle$RQS

(Area of triangle = $\frac{1}{2}\times base \times height$)

= $\frac{1}{2}\times 6 \times 2$ + $\frac{1}{2}\times 6 \times 3$

= $\frac{1}{2}\times 6(2 + 3)$

= $15 cm^2$

Question 10: Sides AB and DC of cyclic quadrilateral ABCD are produced to meet at E, and sides AD and BCare produced to meet at F. If $\angle BAD = 102^\circ$ and $\angle BEC = 38^\circ$ then the difference between $\angle ADC$ and $\angle AFB$ is:

a) $21^\circ$

b) $31^\circ$

c) $22^\circ$

d) $23^\circ$

10) Answer (C)

Solution:

In ΔADE,
∠ADE=180 − (∠AED + ∠EAD)
= 180 − (38 + 102)
= 40$\degree$
⇒∠ADC = 40$\degree$
square ABCD is a cyclic quadrilateral.
∴∠DCB + ∠DAB=180
⇒∠DCB = 180 − ∠DAB
∠DCB = 180 − 102
∠DCB = 78$\degree$
In ΔDFC,
∠DFC=180 – (∠FDC+∠FCD)
∠DFC = 180 − (40 + 78)
∠DFC = 180 − 118
∠DFC = 62$\degree$
∠AFB = ∠DFC = 62$\degree$.

Difference between $\angle BAD$ and $\angle AFB$ = 62 – 40 = 22$\degree$

Question 11: Quadrilateral ABCD circumscribes circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm,then the length of AD is:

a) 6 cm

b) 7.5 cm

c) 7cm

d) 6.8 cm

11) Answer (C)

Solution:

AB = 8 cm

BC = 7 cm

CD = 6 cm

By the property,

AB + CD = BC + AD

8 + 6 = 7 + AC

AC = 14 – 7 = 7 cm

Question 12: ABCD is a cyclic quadrilateral in which AB = 16.5 cm, BC = x cm, CD = 11 cm, AD = 19.8 cm, and BD is bisected by AC at O. What is the value of x ?

a) 12.8 cm

b) 12.4 cm

c) 13.2 cm

d) 13.8 cm

12) Answer (C)

Solution:

ABCD is a cyclic quadrilateral in which AB = 16.5 cm
BC = x cm
CD = 11 cm
AD = 19.8 cm

By the property,

AB⋅BC = AD⋅DC

16.5 $\times x = 19.8 \times 11$

16.5 $\times x = 217.8$

x = 217.8/16.5 = 13.2 cm

Question 13: ABCD is a cyclic quadrilateral. The tangents to the circle at the points A and C on it, intersect at P. If $\angle ABC = 98^\circ$, then what is the measure of $\angle APC$?

a) $22^\circ$

b) $26^\circ$

c) $16^\circ$

d) $14^\circ$

13) Answer (C)

Solution:

ACD is a cyclic quadrilateral so,

$\angle ABC + \angle ADC = 180\degree$

$\angle ADC = 180 – 98 = 82\degree$

$\angle AOC = 2 \times \angle ADC = 2 \times 82 = 164\degree$

In quadrilateral AOCP-

$\angle OAP + \angle APC + \angle PCO + \angle COA = 360\degree$

$\angle OAP = \angle PCO = 90\degree$

($\because$ tangent angle)

$\angle APC = 360 – 90 – 90 – 164 = 16\degree$

Question 14: ABCD is a cyclic quadrilateral in which AB = 15 cm, BC = 12 cm and CD = 10 cm. If AC bisects BD, then what is the measure of AD?

a) 15 cm

b) 13.5 cm

c) 18 cm

d) 20 cm

14) Answer (C)

Solution:

Given ABCD is a cyclic quadrilateral where AB=15,BC= 12,CD =10

is given below diagram

from the above diagram AC bisects BD

$\triangle is similar \triangle BCD

$ \frac{AB}{AD} = \frac{DC}{BC} $

$\Rightarrow \frac{15}{AD} = \frac{10}{12}$

$\Rightarrow AD = \frac{15\times 12} {10} $

$\Rightarrow AD = 18 cm

therefore Option (C) 18 cm Ans

Question 15: From a point P which is at a distance of 10 cm from the centre O of a circle of radius 6 cm, a pair of tangents PQ and PR to the circle at point Q and respectively, are drawn. Then the area of the quadrilateral PQOR is equal to

a) 30 sq.cm

b) 40 sq.cm

c) 24 sq.cm

d) 48 sq.cm

15) Answer (D)

Solution:

From the given question we draw the diagram

From the $ \triangle $

$ x^2 = (10)^2 – (6)^2 $

$ x^2 = 100 – 36 $

$ x^2 = 64$

$ x = 8 $

then area quadrilateral PQOR =$ 2 \times \frac {1}{2} \times 6 \times 8 $

= $ 6\times 8 $

=   $48 cm^2 $ Ans

Question 16: Two equilateral triangles of side $10\sqrt{3}$ cm are joined to form a quadrilateral. What is the altitude of the quadrilateral?

a) 12 cm

b) 14 cm

c) 16 cm

d) i5 cm

16) Answer (D)

Solution:

Given that  $10\sqrt{3}$ cm

We know the area of equilateral triangle = $ \frac{\sqrt {3}} {4} a^2 $   …… Eq (1)

and on the $\triangle DCB   is   also   given = \frac{1}{2} \times a \times h $   …… Eq (2)

then Eq(1) = Eq (2)

$ \frac{\sqrt {3}} {4} a^2  =   \frac{1}{2} \times a \times h $

$\Rightarrow h =  \frac{\sqrt{3}} {2} a $

$\Rightarrow h = \frac{\sqrt{3}} {2} \times 10\sqrt{3}$

$\Rightarrow h = 15 cm Ans

Question 17: ABCD is cyclic quadrilateral. Sides AB and DC, when produced, meet at E, and sides BC and AD, when produced, meet at F. If $\angle$BFA = $60^\circ$ and $\angle$AED = $30^\circ$, then the measure of $\angle$ABC is:

a) $75^\circ$

b) $65^\circ$

c) $80^\circ$

d) $70^\circ$

17) Answer (A)

Solution:

From the given question we draw the diagram is given below

from the above diagram $\angle BFA = 60^\circ , $\angle AFD = 30^\circ $

then $ \angle EBC + \angle ABC = 180^\circ $ (straight line) ………….(1)

$ \angle ABC + \angle ADC = 180^\circ $ (Opposite angle of cyclic quadrilateral)….. (2)

from the above Equestion (1) and (2)

$ \angle EBC + \angle ABC = \angle ABC + \angle ADC $

$\angle EBC = \angle ADC $ …….(3)

$ \angle DFC + \angle DCF + \angle CDF = 180^\circ $ (angle sum property of a triangle) ……. (4)

$ \angle BCE + \angle CBE + \angle CEB = 180^\circ $ (angle sum property of a triangle) ………(5)

from the equestion (4) and (5)

$ \angle DCF = \angle BCF $ (Vertically Opposite angle)

$\angle DFC + \angle DCF + \angle CDF = \angle BCE + \angle CBF + \angle CEB $

$\Rightarrow \angle DFC + \angle CDF = \angle CBF + \angle CEB $

$\Rightarrow 60^\circ + 180^\circ – \angle EBC = \angle EBC + \angle CEB $

$\Rightarrow 60^\circ + 180^\circ = 2 \angle EBC + 30^\circ $

$\Rightarrow 2 \angle EBC = 210^\circ $

$\Rightarrow \angle EBC= 105^\circ $

then $\angle ABC + \angle EBC = 180^\circ $

$\Rightarrow \angle ABC + 105^\circ = 180^\circ $

$\Rightarrow \angle ABC = 180^\circ -105^\circ $

$\Rightarrow \angle ABC = 75^\circ $ Ans

Question 18: In quadrilateral $ABCD, \angle C = 72^\circ$ and $\angle D = 28^\circ$. The bisectors of $\angle A$ and $\angle B$ meet in O. What is the measure of $\angle AOB$?

a) $48^\circ$

b) $54^\circ$

c) $50^\circ$

d) $36^\circ$

18) Answer (C)

Solution:

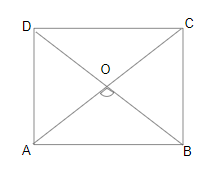
In quadrilateral $ABCD$,
$\angle A + \angle B + \angle C + \angle D$ = 360
$\angle A + \angle B = 360 – 72 – 28 = 260\degree$
$\frac{1}{2}(\angle A + \angle B) = 130\degree$
In $\triangle$ AOB,
$\frac{1}{2}(\angle A + \angle B) + \angle AOB = 180$
$\angle AOB = 180 – 130 = 50\degree$

Question 19: In a circle with centre O, ABCD isa cyclic quadrilateral and AC is the diameter. Chords AB and CD are produced to meet at E. If $\angle CAE = 34^\circ$ and $\angle E = 30^\circ$, then $\angle CBD$ is equal to:

a) $36^\circ$

b) $26^\circ$

c) $24^\circ$

d) $34^\circ$

19) Answer (B)

Solution:

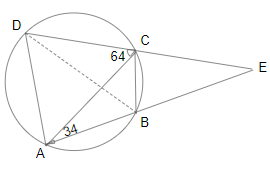
By the exterior angle property,
$\angle DCA$ = 30 + 34 = 64
$\angle DAC$ = 180 – 90 – 64 = 26$\degree$
$\angle DAC = \angle CBD$
$\angle CBD = 26\degree$

Enroll to 15 SSC MTS 2022 Mocks At Just Rs. 149

Download SSC Preparation App

Enroll to 15 SSC CHSL 2022 Mocks At Just Rs. 149