SSC CGL Trigonometry Questions with Solutions PDF

Download SSC CGL Trignometry questions with answers PDF based on previous papers very useful for SSC CGL exams. 20 Very important Trignometry objective questions for SSC exams.

Download SSC CGL Trigonometry Questions with Solutions PDF

Question 1: What is the value of $(cot60^\circ+1/\sqrt{3}) ?$

a) $2\sqrt3$

b) $\frac{\sqrt3}{2}$

c) $\frac{2}{\sqrt3}$

d) $\sqrt3$

Question 2: What is the value of $(\frac{1}{3} – sec 45^\circ)$ ?

a) $\frac{(4-\sqrt3)}{2}$

b) $\frac{(\sqrt{6}-1)}{\sqrt{3}}$

c) $\frac{(1-3\sqrt2)}{3}$

d) $\frac{(\sqrt2-1)}{\sqrt{2}}$

Question 3: ΔABC is right angled at B. If $sec A = \frac{5}{3}$, then what is the value of $cosec C$ ?

a) $\frac{5}{3}$

b) $\frac{3}{4}$

c) $\frac{4}{5}$

d) $\frac{4}{3}$

Question 4: What is the value of $( \frac{1}{\sqrt{3}} + cot 60^\circ)$ ?

a) $\frac{3\sqrt3}{2}$

b) $\frac{7}{2\sqrt{3}}$

c) $\frac{(4+\sqrt3)}{2\sqrt{3}}$

d) $\frac{2}{\sqrt{3}}$

Question 5: ΔABC is right angled at B. If $cot A = \frac{7}{24}$, then what is the value of $cosec C$ ?

a) $\frac{7}{25}$

b) $\frac{25}{7}$

c) $\frac{24}{7}$

d) $\frac{7}{24}$

SSC CGL Previous Papers Download PDF

SSC CGL Free Mock Test

Question 6: What is the value of $(cosec 60^\circ + \frac{1}{2})$ ?

a) $\frac{2}{\sqrt{3}}$

b) $\frac{(2+\sqrt{3})}{2\sqrt{3}}$

c) $\frac{(4+\sqrt{3})}{2\sqrt{3}}$

d) $\frac{(\sqrt{2}+\sqrt{3})}{\sqrt{6}}$

Question 7: ∆DEF is right angled at E. If m$\angle$F = $30^\circ$, then find the value of $(sin D – \frac{1}{3})$.

a) $\frac{-1}{2\sqrt3}$

b) $\frac{(3\sqrt3-2)}{6}$

c) $\frac{(\sqrt{2}-\sqrt3)}{\sqrt{6}}$

d) $\frac{(2\sqrt{2}-1)}{\sqrt{2}}$

Question 8: ∆DEF is right angled at E. If $cosec D = \frac{25}{24}$, then what is the value of $cos F$ ?

a) $\frac{25}{7}$

b) $\frac{24}{7}$

c) $\frac{24}{25}$

d) $\frac{7}{24}$

Question 9: ΔXYZ is right angled at Y. If m∠X = $45^\circ$, then find the value of $(cosec Z +\frac{\sqrt{3}}{2})$.

a) $\frac{(2\sqrt{2}+\sqrt{3})}{2}$

b) $\frac{5}{6}$

c) $\frac{(1+2\sqrt{3})}{2}$

d) $\frac{(\sqrt{2}+1)}{\sqrt{2}}$

Question 10: ΔXYZ is right angled at Y. If $sinX = \frac{4}{5}$, then what is the value of $cos Z$ ?

a) $\frac{3}{4}$

b) $\frac{5}{3}$

c) $\frac{4}{5}$

d) $\frac{4}{3}$

FREE SSC EXAM YOUTUBE VIDEOS

18000+ Questions – Free SSC Study Material

Question 11: What is the value of $(cos 30^\circ + \frac{1}{2})$ ?

a) $\frac{(\sqrt{3}+1)}{\sqrt{3}}$

b) $\frac{(\sqrt{2}+1)}{\sqrt{2}}$

c) $\frac{(\sqrt{3}+1)}{2}$

d) $\frac{(2\sqrt{3}+1)}{\sqrt{3}}$

Question 12: ΔDEF is right angled at E. If $cosec D = \frac{5}{4}$, then what is the value of $cosec F$ ?

a) $\frac{5}{3}$

b) $\frac{3}{4}$

c) $\frac{4}{5}$

d) $\frac{4}{3}$

Question 13: What is the value of $(2 – tan 60^\circ)$ ?

a) $\frac{-1}{\sqrt{3}}$

b) $\frac{(\sqrt{3}-4)}{2\sqrt{3}}$

c) $\frac{-1}{2}$

d) $2-\sqrt3$

Question 14: ΔUVW is right angled at V. If $sin U = \frac{24}{25}$, then what is the value of $cosW$ ?

a) $\frac{25}{7}$

b) $\frac{24}{7}$

c) $\frac{7}{24}$

d) $\frac{24}{25}$

Question 15: ΔPQR is right angled at Q. If m$\angle$P = 60°, then find the value of $(cot R + \frac{\sqrt{3}}{2})$.

a) $\frac{3\sqrt3}{2}$

b) $1+\sqrt3$

c) $\frac{(2\sqrt2+1)}{2}$

d) $\frac{(3\sqrt3+1)}{6}$

SSC CGL Free Mock Test

Question 16: ΔABC is right angled at B. If $cot A = \frac{8}{15}$, then what is the value of $cos C$ ?

a) ${15}{8}$

b) $\frac{8}{17}$

c) $\frac{17}{15}$

d) $\frac{15}{17}$

Question 17: What is the value of $(cos 45^\circ – \frac{1}{3})$ ?

a) $2-\sqrt3$

b) $\frac{2}{\sqrt{3}}$

c) $\frac{(3-\sqrt2)}{3\sqrt{2}}$

d) $\frac{1}{2\sqrt{3}}$

Question 18: ΔUVW is right angled at V. If $sec U = \frac{5}{3}$, then what is the value of $tan W$ ?

a) $\frac{3}{4}$

b) $\frac{5}{3}$

c) $\frac{4}{5}$

d) $\frac{4}{3}$

Question 19: ΔDEF is right angled at E. If m$\angle$F = $30^\circ$, then find the value of $(cos D – \frac{1}{\sqrt2})$

a) $\frac{-1}{2}$

b) $\frac{(\sqrt{6}-1)}{\sqrt{3}}$

c) $\frac{(\sqrt{2}-2)}{2\sqrt{2}}$

d) $\sqrt{3}-2$

Question 20: ∆PQR is right angled at Q. If m$\angle$P = $60^\circ$, then find the value of $(sec R + \frac{1}{2})$

a) $\frac{(2\sqrt{2}+\sqrt{3})}{2}$

b) $\frac{(\sqrt{3}+4)}{2\sqrt{3}}$

c) $\sqrt{3}+2$

d) $\frac{5}{6}$

100+ Free GK Tests for SSC Exams

Download Free GK PDF

Answers & Solutions:

1) Answer (C)

Expression : $(cot60^\circ+1/\sqrt{3})$

= $\frac{1}{\sqrt3}+\frac{1}{\sqrt3}$

= $\frac{2}{\sqrt3}$

=> Ans – (C)

2) Answer (C)

Expression : $(\frac{1}{3} – sec 45^\circ)$

= $\frac{1}{3}-\sqrt2$

= $\frac{(1-3\sqrt2)}{3}$

=> Ans – (C)

3) Answer (A)

Given : $\sec A$ = $\frac{5}{3}$

Also, $\sec A=\frac{AC}{AB}=\frac{5}{3}$

Let AC = 5 cm and AB = 3 cm

To find : $\cosec C=\frac{AC}{AB}$

= $\frac{5}{3}$

=> Ans – (A)

4) Answer (D)

Expression : $( \frac{1}{\sqrt{3}} + cot 60^\circ)$

= $\frac{1}{\sqrt3}+\frac{1}{\sqrt3}$

= $\frac{2}{\sqrt{3}}$

=> Ans – (D)

5) Answer (B)

Given : $\cot A$ = $\frac{7}{24}$

Also, $\cot A=\frac{AB}{BC}=\frac{7}{24}$

Let AB = 7 cm and BC = 24 cm

Thus, in $\triangle$ ABC,

=> $(AC)^2=(AB)^2+(BC)^2$

=> $(AC)^2=(7)^2+(24)^2$

=> $(AC)^2=49+576=625$

=> $AC=\sqrt{625}=25$ cm

To find : $\cosec C=\frac{AC}{AB}$

= $\frac{25}{7}$

=> Ans – (B)

6) Answer (C)

Expression : $(cosec 60^\circ + \frac{1}{2})$

= $\frac{2}{\sqrt3}+\frac{1}{2}$

= $\frac{(4+\sqrt{3})}{2\sqrt{3}}$

=> Ans – (C)

7) Answer (B)

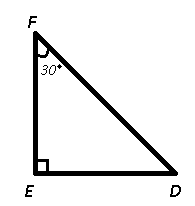
Sum of angles of $\triangle$ DEF = $\angle D+\angle E+\angle F=180^\circ$

=> $\angle D+90^\circ+30^\circ=180^\circ$

=> $\angle D=180^\circ-120^\circ=60^\circ$

To find : $(sin D – \frac{1}{3})$

= $sin(60^\circ)-\frac{1}{3}$

= $\frac{\sqrt3}{2}-\frac{1}{3}$

= $\frac{(3\sqrt3-2)}{6}$

=> Ans – (B)

8) Answer (C)

Given : $\cosec D$ = $\frac{25}{24}$

Also, $\cosec D=\frac{DF}{EF}=\frac{25}{24}$

Let DF = 25 cm and EF = 24 cm

To find : $\cos F=\frac{EF}{DF}$

= $\frac{24}{25}$

=> Ans – (C)

9) Answer (A)

Sum of angles of $\triangle$ XYZ = $\angle X+\angle Y+\angle Z=180^\circ$

=> $45^\circ+90^\circ+\angle Z=180^\circ$

=> $\angle X=180^\circ-135^\circ=45^\circ$

To find : $(cosec Z +\frac{\sqrt{3}}{2})$

= $cosec(45^\circ)+\frac{\sqrt3}{2}$

= $\sqrt2+\frac{\sqrt3}{2}$

= $\frac{(2\sqrt{2}+\sqrt{3})}{2}$

=> Ans – (A)

10) Answer (C)

Given : $\sin X$ = $\frac{4}{5}$

Also, $\sin X=\frac{YZ}{XZ}=\frac{4}{5}$

Let YZ = 4 cm and XZ = 5 cm

To find : $\cos Z=\frac{YZ}{XZ}$

= $\frac{4}{5}$

=> Ans – (C)

Free SSC Daily Practice Set

11) Answer (C)

Expression : $(cos 30^\circ + \frac{1}{2})$

= $\frac{\sqrt3}{2}+\frac{1}{2}$

= $\frac{(\sqrt{3}+1)}{2}$

=> Ans – (C)

12) Answer (A)

Given : $\cosec D$ = $\frac{5}{4}$

Also, $\cosec D=\frac{DF}{EF}=\frac{5}{4}$

Let DF = 5 cm and EF = 4 cm

Thus, in $\triangle$ DEF, => $(DE)^2=(DF)^2-(EF)^2$

=> $(DE)^2=(5)^2-(4)^2$

=> $(DE)^2=25-16=9$

=> $DE=\sqrt{9}=3$ cm

To find : $\cosec F=\frac{DF}{DE}$

= $\frac{5}{3}$

=> Ans – (A)

13) Answer (D)

Expression : $(2 – tan 60^\circ)$

We know that, $tan (60^\circ)=\sqrt3$

= $2-\sqrt3$

=> Ans – (D)

14) Answer (D)

 

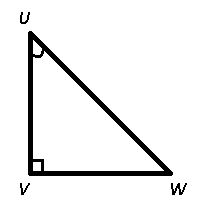
Given : $\sin U$ = $\frac{24}{25}$

Also, $\sin U=\frac{VW}{UW}=\frac{24}{25}$

Let VW = 24 cm and UW = 25 cm

To find : $\cos W=\frac{VW}{UW}$

= $\frac{24}{25}$

=> Ans – (D)

15) Answer (A)

Sum of angles of $\triangle$ PQR = $\angle P+\angle Q+\angle R=180^\circ$

=> $60^\circ+90^\circ+\angle R=180^\circ$

=> $\angle R=180^\circ-150^\circ=30^\circ$

To find : $(cot R + \frac{\sqrt{3}}{2})$

= $cot(30^\circ)+\frac{\sqrt3}{2}$

= $\sqrt3+\frac{\sqrt3}{2}$

= $\frac{3\sqrt3}{2}$

=> Ans – (A)

16) Answer (D)

Given : $\cot A$ = $\frac{8}{15}$

Also, $\cot A=\frac{AB}{BC}=\frac{8}{15}$

Let AB = 8 cm and BC = 15 cm

Thus, in $\triangle$ ABC,

=> $(AC)^2=(AB)^2+(BC)^2$

=> $(AC)^2=(8)^2+(15)^2$

=> $(AC)^2=64+225=289$

=> $AC=\sqrt{289}=17$ cm

To find : $\cos C=\frac{BC}{AC}$

= $\frac{15}{17}$

=> Ans – (D)

17) Answer (C)

Expression : $(cos 45^\circ – \frac{1}{3})$

= $\frac{1}{\sqrt2}-\frac{1}{3}$

= $\frac{(3-\sqrt2)}{3\sqrt{2}}$

=> Ans – (C)

18) Answer (A)

 

Given : $\sec U$ = $\frac{5}{3}$

Also, $\sec U=\frac{UW}{UV}=\frac{5}{3}$

Let UW = 5 cm and UV = 3 cm

Thus, in $\triangle$ UVW, => $(VW)^2=(UW)^2-(UV)^2$

=> $(VW)^2=(5)^2-(3)^2$

=> $(VW)^2=25-9=16$

=> $VW=\sqrt{16}=4$ cm

To find : $\tan W=\frac{UV}{VW}$

= $\frac{3}{4}$

=> Ans – (A)

19) Answer (C)

Sum of angles of $\triangle$ DEF = $\angle D+\angle E+\angle F=180^\circ$

=> $\angle D+90^\circ+30^\circ=180^\circ$

=> $\angle D=180^\circ-120^\circ=60^\circ$

To find : $(cos D – \frac{1}{\sqrt2})$

= $cos(60^\circ)-\frac{1}{\sqrt2}$

= $\frac{1}{2}-\frac{1}{\sqrt2}$

= $\frac{(\sqrt{2}-2)}{2\sqrt{2}}$

=> Ans – (C)

20) Answer (B)

Sum of angles of $\triangle$ PQR = $\angle P+\angle Q+\angle R=180^\circ$

=> $60^\circ+90^\circ+\angle R=180^\circ$

=> $\angle R=180^\circ-150^\circ=30^\circ$

To find : $(sec R + \frac{1}{2})$

= $sec(30^\circ)+\frac{1}{2}$

= $\frac{2}{\sqrt3}+\frac{1}{2}$

= $\frac{(\sqrt{3}+4)}{2\sqrt{3}}$

=> Ans – (B)

SSC Free Previous Papers App