SSC CGL Expected Quant Questions 2019
Download SSC CGL Expected Quant Questions 2019 PDF based on previous papers very useful for SSC CGL exams. 20 Expected Quant Questions for SSC exams.
Download SSC CGL Expected Quant Questions
10 SSC CGL Mocks – Just Rs. 117
Question 1: Find the value of $\frac{(\cot\theta-cosec\theta+1)(\tan\theta+\sec\theta+1)}{\cos\theta cosec\theta}?$
a) $2\cos\theta$
b) 2
c) $2cot\theta$
d) $2tan\theta$
Question 2: What is the value of $sec12^{0}sin12^{0}tan38^{0}tan78^{0}tan52^{0}$?
a) 1
b) 3
c) $\frac{1}{2}$
d) $\frac{3}{2}$
Question 3: What is the value of $\frac{\cos x+cos y}{sinx + siny}$ ?
a) $\tan\frac{x+y}{2}$
b) $\tan\frac{x-y}{2}$
c) $\cot\frac{x-y}{2}$
d) $\cot\frac{x+y}{2}$
Question 4: If sin $x=\frac{1}{2}$ and cos $y=\frac{1}{2}$, what is the value of sin(x+y)?
a) $\frac{2}{3}$
b) $\frac{4}{9}$
c) $\frac{5}{9}$
d) 1
Question 5: What is the value of $\frac{(\tan^{2}x-\sin^{2}x)}{\sec^{2}x}$ ?
a) $\sin^{4}x$
b) $\cos^{2}x$
c) $\sin^{2}x$
d) $cos^{4}x$
SSC CGL Previous Papers Download PDF
Question 6: In the given figure, what is the value of $\angle1+\angle2+\angle3+\angle4+\angle5+\angle6+\angle7+\angle8+\angle9+\angle10$?
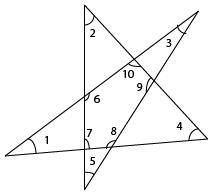
a) 600
b) 720
c) 900
d) 1080
Question 7: AB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, the what is the length (in cm.) of OA ?
a) 25
b) 26
c) 28
d) 31
Question 8: In $\triangle$PQR, S and T are the mid points of sides PQ and PR respectively. If $\angle$QPR = $45^{0}$ and $\angle$PRQ = $55^{0}$, then what is the value (in degrees) of $\angle$QST ?
a) 80
b) 85
c) 90
d) 100
Question 9: A,B and C are the three points on a circle such that $\angle$ABC = $35^{0}$ and $\angle$BAC = $85^{0}$. What is the angle (in degrees) subtended by arc AB at the center of the circle?
a) 60
b) 90
c) 135
d) 120
Question 10: A circle passing through points Q and R of triangle PQR, cuts the sides PQ and PR at points X and Y respectively. If PQ = PR, then what is the value (in degrees) of $\angle$PRQ + $\angle$QXY ?
a) 120
b) 150
c) 240
d) 180
18000+ Questions – Free SSC Study Material
Question 11: If $x^{2}-9x-1=0$, then what is the value of $ (x^{2}-\frac{1}{x^{2}}+5x-\frac{5}{x})$ ?
a) 115
b) 128
c) 124
d) 133
Question 12: If $(x-\frac{1}{x})=3$, then what is the value of $(x^{3}-\frac{1}{x^{3}})$ ?
a) 36
b) 21
c) 9
d) 27
Question 13: If $(3x^{2}-9x+3)=0$, then what is the value of $(x+\frac{1}{x})^{3}$ ?
a) 9
b) 729
c) 81
d) 27
Question 14: If $a^{2}+b^{2}+c^{2}+\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=6$, then what is the value of $(a^{2}+b^{2}+c^{2})$ ?
a) 3
b) 6
c) -3
d) 2
Question 15: If $x=17-4\sqrt{18}$, then find the value of $(\sqrt{x}+\frac{1}{\sqrt{x}})$ ?
a) $7\sqrt{2}$
b) 9
c) 22
d) 6
Question 16: If the ratio of volume of two cubes is 11 : 13, then what is the ratio of the sides of the two cubes ?
a) 11 : 13
b) 121 : 169
c) $(11)^{\frac{1}{2}}:(13)^{\frac{1}{2}}$
d) $(11)^{\frac{1}{3}}:(13)^{\frac{1}{3}}$
Question 17: If the diameter of a sphere is 14 cm., then what is the curved surface area (in $cm.^{2}$) of the sphere?
a) 616
b) 1232
c) 2464
d) 576
Question 18: The difference between circumference and the radius of a circle is 111 cm. What is the area (in $cm^{2}$) of the circle?
a) 469
b) 1386
c) 912
d) 1086
Question 19: Three circles of radius 9 cm are kept touching each other. The string is tightly tied around the three circles. What is the length (in cm.) of the string ?
a) $48+18\pi$
b) $48+24\pi$
c) $54+18\pi$
d) $54+24\pi$
Question 20: The perimetre of a rhombus in 20 cm and one of the diagonal is 8 cm. What is the area (in $cm^{2}$) of the rhombus?
a) 12
b) 24
c) 48
d) 96
Answers & Solutions:
1) Answer (D)
Expression : $\frac{(\cot\theta-cosec\theta+1)(\tan\theta+\sec\theta+1)}{\cos\theta cosec\theta}$
= $\frac{sin\theta}{cos\theta}\times[(\frac{cos\theta}{sin\theta}-\frac{1}{sin\theta}+1)\times(\frac{sin\theta}{cos\theta}+\frac{1}{cos\theta}+1)]$
= $\frac{sin\theta}{cos\theta}\times[(\frac{cos\theta+sin\theta-1}{sin\theta})\times(\frac{cos\theta+sin\theta+1}{cos\theta})]$
Using, $(x-y)(x+y)=x^2-y^2$, where $x=cos\theta+sin\theta$ and $y=1$
= $\frac{1}{cos^2\theta}\times[(cos\theta+sin\theta)^2-(1)^2]$
= $\frac{1}{cos^2\theta}\times[cos^2\theta+sin^2\theta+2cos\theta.sin\theta-1]$
= $\frac{1}{cos^2\theta}\times[1+2cos\theta.sin\theta-1]$
= $\frac{1}{cos^2\theta}\times(2cos\theta.sin\theta)$
= $\frac{2sin\theta}{cos\theta}=2tan\theta$
=> Ans – (D)
2) Answer (A)
Expression : $sec12^{0}sin12^{0}tan38^{0}tan78^{0}tan52^{0}$
= $\frac{1}{cos(12^\circ)}.sin(12^\circ).tan(38^\circ).tan(78^\circ).tan(52^\circ)$
= $[tan(12^\circ).tan(78^\circ)].[tan(38^\circ).tan(52^\circ)]$
Using, $tan(90^\circ-\theta)=cot(\theta)$
= $[tan(12^\circ).cot(12^\circ)].[tan(38^\circ).cot(38^\circ)]$
Also, $tan(\theta)cot(\theta)=1$
= $1\times1=1$
=> Ans – (A)
3) Answer (D)
Expression : $\frac{\cos x+cos y}{sinx + siny}$
= $\frac{cos(\frac{x+y}{2})cos(\frac{x-y}{2})}{sin(\frac{x+y}{2})cos(\frac{x-y}{2})}$
= $\frac{cos(\frac{x+y}{2})}{sin(\frac{x+y}{2})}$
= $cot(\frac{x+y}{2})$
=> Ans – (D)
4) Answer (D)
Given : $sin x=\frac{1}{2}$ and $cos y=\frac{1}{2}$
=> $sin(x)=sin(30^\circ)$
=> $x=30^\circ$
Similarly, => $cos(y)=cos(60^\circ)$
=> $y=60^\circ$
$\therefore$ $sin(x+y)$
= $sin(30^\circ+60^\circ)=sin(90^\circ)=1$
=> Ans – (D)
5) Answer (A)
Expression : $\frac{(\tan^{2}x-\sin^{2}x)}{\sec^{2}x}$
= $\frac{(\frac{sin^{2}x}{cos^2x}-sin^{2}x)}{sec^{2}x}$
= $\frac{sin^2x}{sec^2x}(\frac{1}{cos^2x}-1)$
= $sin^2x cos^2x(\frac{1-cos^2x}{cos^2x})$
= $sin^2x\times(sin^2x)=sin^4x$
=> Ans – (A)
6) Answer (B)
7) Answer (A)
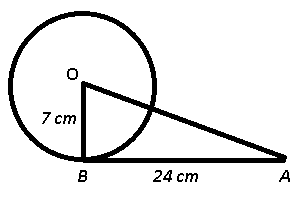
Given : OB is radius of circle = 7 cm and tangent AB = 24 cm
To find : OA = ?
Solution : The radius of a circle intersects the tangent at right angle, => $\angle OBA = 90^\circ$
Thus in $\triangle$ OAB,
=> $(OA)^2=(OB)^2+(AB)^2$
=> $(OA)^2=(7)^2+(24)^2$
=> $(OA)^2=49+576=625$
=> $OA=\sqrt{625}=25$ cm
=> Ans – (A)
8) Answer (D)
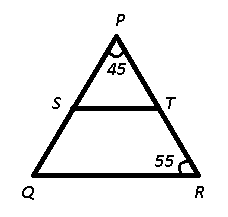
Given : $\angle$QPR = $45^\circ$ and $\angle$PRQ = $55^\circ$
To find : $\angle$QST = ?
Solution : In triangle, PQR
=> $\angle P+\angle Q+\angle R=180^\circ$
=> $45^\circ+55^\circ+\angle Q=180^\circ$
=> $\angle Q=180^\circ-100^\circ=80^\circ$
Now, since ST divides PQ and PR equally, thus ST is parallel to QR.
$\therefore$ Angles on the same side of transversal are supplementary, => $\angle PQR+\angle QST=180^\circ$
=> $\angle QST=180^\circ-80^\circ=100^\circ$
=> Ans – (D)
9) Answer (D)
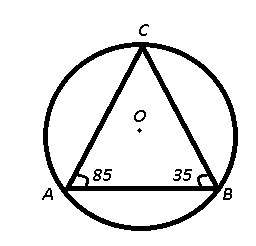
Given : $\angle$ABC = $35^\circ$ and $\angle$BAC = $85^\circ$
To find : $\angle$ AOB = ?
Solution : In triangle, ABC
=> $\angle A+\angle B+\angle C=180^\circ$
=> $85^\circ+35^\circ+\angle C=180^\circ$
=> $\angle C=180^\circ-120^\circ=60^\circ$
Now, angle subtended by an arc at the centre is double the angle subtended by it at any point on the circle.
=> $\angle AOB=2\times\angle ACB$
= $2\times60^\circ=120^\circ$
=> Ans – (D)
10) Answer (D)
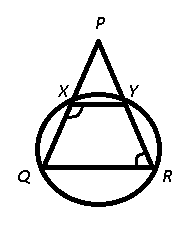
Given : PQR is an isosceles triangle, PQ = PR
To find : $\angle$PRQ + $\angle$QXY = ?
Solution : Since, $\triangle$ PQR is isosceles, we have $\angle Q=\angle R$
Now, XY is parallel to QR, and sum of angles on the same side of transversal is supplementary, => $\angle PQR+\angle QXY=180^\circ$
=> $\angle$PRQ + $\angle$QXY = $180^\circ$
II method : XYRQ is a cyclic quadrilateral and opposite angles in a cyclic quadrilateral are supplementary.
=> Ans – (D)
11) Answer (B)
Given : $x^{2}-9x-1=0$
=> $x^2-1=9x$
Dividing both sides by $’x’$,
=> $x-\frac{1}{x}=9$ ————–(i)
Squaring both sides, we get :
=> $(x-\frac{1}{x})^2=(9)^2$
=> $x^2-\frac{1}{x^2}-2(x)(\frac{1}{x})=81$
=> $x^2-\frac{1}{x^2}=81+2=83$ ———–(ii)
$\therefore$ $ (x^{2}-\frac{1}{x^{2}}+5x-\frac{5}{x})$
= $ (x^{2}-\frac{1}{x^{2}})+5(x-\frac{1}{x})$
Substituting values from equation (i) and (ii),
= $83+5(9)=128$
=> Ans – (B)
12) Answer (A)
Given : $(x-\frac{1}{x})=3$ ———-(i)
Cubing both sides, we get :
=> $(x-\frac{1}{x})^3=(3)^3$
=> $x^3-\frac{1}{x^3}-3(x)(\frac{1}{x})(x-\frac{1}{x})=27$
=> $x^3-\frac{1}{x^3}-3(1)(3)=27$
=> $(x^{3}-\frac{1}{x^{3}})=27+9=36$
=> Ans – (A)
13) Answer (D)
Given : $(3x^{2}-9x+3)=0$
=> $(3x^{2}+3)=9x$
Dividing both sides by $’3x’$, we get :
=> $x+\frac{1}{x}=3$ ————-(i)
Cubing both sides,
=> $(x+\frac{1}{x})^3=(3)^3$
=> $(x+\frac{1}{x})^3=27$
=> Ans – (D)
14) Answer (A)
Given : $a^{2}+b^{2}+c^{2}+\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=6$
=> $(a^2+\frac{1}{a^2}-2)+(b^2+\frac{1}{b^2}-2)+(c^2+\frac{1}{c^2}-2)=0$
=> $(a-\frac{1}{a})^2+(b-\frac{1}{b})^2+(c-\frac{1}{c})^2=0$
$\because$ Sum of three positive terms is zero, hence each term is equal to 0.
=> $(a-\frac{1}{a})=$ $(b-\frac{1}{b})=$ $(c-\frac{1}{c})=0$
=> $\frac{a^2-1}{a}=0$
=> $a^2=1$
Similarly, $b^2=c^2=1$
$\therefore$ $(a^{2}+b^{2}+c^{2})=1+1+1=3$
=> Ans – (A)
15) Answer (D)
Expression : $x=17-4\sqrt{18}$
=> $x=17-2\sqrt{72}$
=> $x=(\sqrt9)^2+(\sqrt8)^2+2(\sqrt9)(\sqrt8)$
Using, $a^2+b^2+2ab=(a+b)^2$
=> $x=(\sqrt9+\sqrt8)^2$
=> $\sqrt{x}=3+2\sqrt2$ ————-(i)
Also, $\frac{1}{\sqrt{x}}=\frac{1}{3+2\sqrt2}$
Rationalizing the denominator, we get :
=> $\frac{1}{\sqrt{x}}=\frac{1}{3+2\sqrt2}\times(\frac{3-2\sqrt2}{3-2\sqrt2})$
=> $\frac{1}{\sqrt{x}}=\frac{3-2\sqrt2}{9-8}$
=> $\frac{1}{\sqrt{x}}=3-2\sqrt2$ ———(ii)
Adding equation (i) and (ii),
$\therefore$ $(\sqrt{x}+\frac{1}{\sqrt{x}})=(3+2\sqrt2)+(3-2\sqrt2)=6$
=> Ans – (D)
16) Answer (D)
Let side of the two cubes be $a$ and $b$ units respectively
Ratio of volumes = $\frac{a^3}{b^3}=\frac{11}{13}$
=> $\frac{a}{b}=(\sqrt[3]{\frac{11}{13}})$
=> $\frac{a}{b}=(11)^{\frac{1}{3}}:(13)^{\frac{1}{3}}$
=> Ans – (D)
17) Answer (A)
Radius of sphere = 7 cm
Curved surface area = $4\pi r^2$
= $4\times\frac{22}{7}\times(7)^2=616$ $cm^2$
=> Ans – (A)
18) Answer (B)
Let radius of circle = $r$ cm
=> $2\pi r-r=111$
=> $r(2\times\frac{22}{7}-1)=111$
=> $r\times\frac{44-7}{7}=111$
=> $r=111\times\frac{7}{37}=21$ cm
$\therefore$ Area of circle = $\pi r^2$
= $\frac{22}{7}\times(21)^2=1386$ $cm^2$
=> Ans – (B)
19) Answer (C)
20) Answer (B)
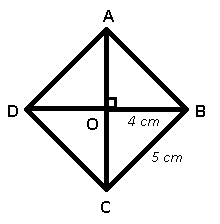
Given : ABCD is the rhombus whose diagonals bisect at O and the diagonals of a rhombus bisect each other at right angle. BD = 8 cm
=> OB = 4 cm
Perimeter of rhombus = 20 cm
=> BC = $\frac{20}{4}=5$ cm
Thus, in $\triangle$ BOC,
=> $(OC)^2=(BC)^2-(OB)^2$
=> $(OC)^2 = (5)^2-(4)^2$
=> $(OC)^2=25-16=9$
=> $OC=\sqrt{9}=3$ cm
Thus, AC = 6 cm and BD = 8 cm
$\therefore$ Area of rhombus = $\frac{1}{2}\times d_1\times d_2$
= $\frac{1}{2}\times6\times8=24$ $cm^2$
=> Ans – (B)
We hope this Expected Quant questions for SSC Exam will be highly useful for your preparation.





