Percentage Questions For SSC MTS
Download Top-20 SSC MTS Percentage Questions PDF. Percentage questions based on asked questions in previous year exam papers very important for the SSC MTS exam.
Download Percentage Questions For SSC MTS
Take a free mock test for SSC MTS
SSC MTS Previous Papers (Download PDF)
Instructions
Question 1: A number is increased by 10% and then decreased by 10% then by what percent should the value be increased to get the original value ?
a) 0 %
b) 100/99 %
c) 1%
d) 99/100 %
Question 2: A 20 litre mixture contains 60% of alcohol and 4 litres of alcohol is added to it then what is the water percentage in the mixture ?l
a) 33.33%
b) 20%
c) 40%
d) 25%
Question 3: A number is increased by 20% and then decreased by 30%. What is the percentage change in the value ?
a) 16%
b) 24%
c) 20%
d) 28%
Question 4: A batsman scored 168 runs which included 3 boundaries and 5 sixes. How much percentage of his total score did he make by running between the wickets?
a) 60%
b) 75%
c) 80%
d) 50%
Question 5: In a school, Class A has 30% boys, Class B has 40% girls. Then, the number of girls in Class A is what percentage of the number of boys in Class B?
a) 2.5%
b) 4%
c) 15%
d) Can’t be determined
Take a free mock test for SSC MTS
Question 6: The price of sugar is increased by 40%. By how much percent should there be reduction in consumption so that the expenditure remains the same?
a) 28.5%
b) 32.5%
c) 42%
d) 40%
Question 7: Find the percentage change in area of a rectangle if the length of the rectangle is reduced by 20% and breadth of the rectangle is increased by 10%.
a) 28% increase
b) 88% decrease
c) 12% increase
d) 18% decrease
Question 8: If a shopkeeper gives three successive discounts of 20% each, then what is the effective discount percentage?
a) 48.8%
b) 62.5%
c) 37.8%
d) 69.8%
Question 9: The price of rice has increased by 50%. By how much percent should there be reduction in consumption so that the expenditure remains the same?
a) 33.33%
b) 50%
c) 66.67%
d) 63.33%
Question 10: The price of sugar has increased by 25%. By how much percent should there be a reduction in consumption so that the expenditure remains the same?
a) 25%
b) 20%
c) 33.33%
d) 40%
SSC Study Material (18000 Solved Questions)
General Science Notes for SSC Exams
Question 11: Amit scored 20% marks and failed by 15 marks. Rohit scored 40% marks and obtained 25 marks more than those required to pass. Then find the pass percentage.
a) 35%
b) 37.5%
c) 27.5%
d) 24.75%
Question 12: If a% of b=20 and b% of c=30 then how much percent is c greater than a ?
a) 50%
b) 150%
c) 75%
d) 66.66%
Instructions
The given pie chart shows the marks obtained (in degrees) by a student in different subjects. The total marks obtained by the student in the examination is 432.

Question 13: If the maximum marks per subject is 100, then what is the total marks (in percentage) obtained in English and Hindi together?
a) 168
b) 68
c) 76
d) 84
Question 14: The marks obtained in science is what percentage of the total marks?
a) 20.14
b) 18.12
c) 17.16
d) 19.44
Instructions
The table give below shows the marks obtained by six students in 5 different subjects.

Question 15: What is the aggregate percentage of marks obtained by student C in all the five subjects?
a) 71
b) 75
c) 76
d) 73
Instructions
The line chart given below represents the sales (in 00) of trousers and shirts for five months.

Question 16: What is the percentage increase in the sales of the trousers from January to February?
a) 25
b) 20
c) 10
d) 28
Question 17: An article having marked price Rs 1800 is sold for Rs 1476. What is the discount percentage?
a) 14
b) 15
c) 16
d) 18
Instructions
The following pie chart shows the expenditure (in percentage) of five companies P, Q, R, S and T in the year 2016. Total Expenditure = 48 crores.
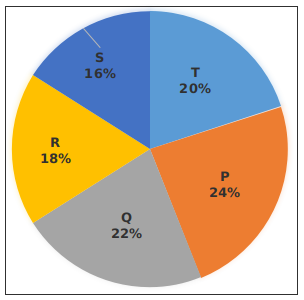
Question 18: Total amount spent by company S is what percent of total amount spent by company T and R?
a) 42.1
b) 43
c) 39.68
d) 41
Question 19: By how much percent expenditure of company Q and R together greater than that of company P?
a) 33.33
b) 60
c) 66.67
d) 75
Question 20: What was the total expenditure (in Rs crores) of the company Q, R and T together?
a) 19.2
b) 28.8
c) 24.3
d) 31.4
200+ SSC Important Practice Sets
General Knowledge Q&A for Competitive Exams (Download PDF)
Answers & Solutions:
1) Answer (B)
let the value be x
Increased by 10% it becomes 1.1x
Decreased by 10% it becomes 1.1x*0.9
=0.99x
Percentage to be increased to get the original value=(0.01x/0/0.99x)*100
=100/99 %
2) Answer (A)
In a 20 litre mixture alcohol percent =60%
Therefore 20*60/100=12 litres
Water =20-12=8 litres
Total alcohol=12+4=16 litres
Water percentage=(8/24)*100
=33.33%
3) Answer (A)
let the number be x
As it is increased by 20% we have x*1.2=1.2x
And again decreased by 30% and so 1.2x*0.7=0.84x
Percentage change in the value ((x-0.84x)/x)*100=16%
4) Answer (B)
Score he made using boundaries and sixes = 4*3+5*6 = 12+30 = 42 runs
Total score = 168 runs
Score made by running between the wickets = 168-42 = 126 runs
Therefore, Required percentage = $\dfrac{126}{168} \times 100 = 75$%
5) Answer (D)
Let the total number of students in Class A be A.
Then, Boys in Class A = 30% of A = 0.3A
Then, Girls in Class A = A – 0.3A = 0.7A
Let the total number of students in Class B be B.
Then, Girls in Class B = 40% of B = 0.4B
Then, Boys in Class B = B – 0.4B = 0.6B
Therefore, Required percentage = $\dfrac{0.7A}{0.6B} \times 100$
Since, the total number of students in Class A and Class B is unknown, the required percentage can’t be determined.
6) Answer (A)
Let the initial price of sugar be Rs.100
Let the initial consumption be 100 kg.
Then Initial expenditure $= 100\times100$
New price = 140% of Rs.100 = Rs140
Let the final consumption be Rs.x
Initial expenditure = Final expenditure
$100\times100 = 140\times x$
⇒ x = 71.42 kg
Percentage Reduction in consumption = $\dfrac{100-71.42}{100}\times 100 = 28.58$%
7) Answer (C)
Effective change in percentage $= l+b+\dfrac{l \times b}{100} = -20+10+\dfrac{(-20)\times (10)}{100} = -10-2 = -12$%
Negative indicates decrease in percentage. Hence, the area decreases by 12%
8) Answer (A)
Let the Marked price be Rs.1000
Selling price after three successive discounts = $1000 \times \dfrac{80}{100}\times \dfrac{80}{100}\times \dfrac{80}{100} = Rs.512$
Effective discount = $\dfrac{1000-512}{1000} \times 100 = 48.8$%
9) Answer (C)
Let the initial price be Rs.100
Let the initial consumption be 100 kg
Price increased by 50%
Final price = 150% of Rs.100 = Rs.150
Let final consumption be x kg
Initial expenditure = Final expenditure
⇒ $100\times100 = 150\times x$
⇒ $x = \dfrac{200}{3} = 66.67$
Final consumption $= 66.67$ kg
Percentage Reduction in consumption $= \dfrac{100-66.67}{100}\times 100 = 33.33$%
10) Answer (B)
Let the initial price be Rs.100
Let the initial consumption be 100 kg
Price increased by 25%
Final price = 125% of Rs.100 = Rs.125
Let final consumption be x kg
Initial expenditure = Final expenditure
⇒ $100\times100 = 125\times x$
⇒ $x = 80$
Final consumption $= 80$ kg
Percentage Reduction in consumption $= \dfrac{100-80}{100}\times 100 = 20$%
11) Answer (C)
Let the maximum marks be ‘x’
Then, Pass marks = 20% of x + 15 = 40% of x – 25
⇒ 0.2x+15 = 0.4x-25
⇒ 0.2x = 40
⇒ x = 200
Hence, Maximum marks = 200
Pass marks = 20% of 200+15 = 40+15 = 55
Pass percentage $= \dfrac{55}{200}\times 100 = 27.5$%
12) Answer (A)
Given ab=2000
bc=3000
Then $\frac{ab}{bc}$=$\frac{2000}{3000}$
$\frac{a}{c}$=$\frac{2}{3}$
c=$\frac{3}{2}$ $\times a$
Required percentage =$\frac{(\frac{3}{2}) a -a}{a}$ $\times 100$
=50%
13) Answer (D)
Total marks in the examination = 432
Marks (in degree) obtained in English and Hindi together = $75+65=140^\circ$
Marks obtained in English and Hindi together = $\frac{140^\circ}{360^\circ}\times432=168$
$\therefore$ Total marks (in percentage) obtained in English and Hindi together = $\frac{168}{200}\times100=84\%$
=> Ans – (D)
14) Answer (D)
Marks (in degrees) obtained in Science = $70^\circ$
Total marks (in degrees) = $360^\circ$
=> Required % = $\frac{70}{360}\times100$
= $\frac{700}{36}=19.44\%$
=> Ans – (D)
15) Answer (D)
Total marks obtained by student C
= 68 + 79 + 55 + 91 + 72 = 365
=> Average marks = $\frac{365}{5}=73$
=> Ans – (D)
16) Answer (A)
Sale of trousers in January (in ’00) = 40
Sale of trousers in February (in ’00) = 50
=> Required % increase = $\frac{(50-40)}{40}\times100$
= $\frac{1000}{40}=25\%$
=> Ans – (A)
17) Answer (D)
Marked price of article = Rs. 1800
Selling price = Rs. 1476
=> Discount % = $\frac{(1800-1476)}{1800}\times100$
= $\frac{324}{18}=18\%$
=> Ans – (D)
18) Answer (A)
% amount spent by company S = 16%
% amount spent by company T and R = (20+18) = 38%
=> Required percent spent by company S = $\frac{16}{38}\times100$
= $\frac{800}{19}=42.1\%$
=> Ans – (A)
19) Answer (C)
% amount spent by company P = 24%
% amount spent by company Q and R = (22+18) = 40%
=> Required percent = $\frac{(40-24)}{24}\times100$
= $\frac{2}{3}\times100=66.67\%$
=> Ans – (C)
20) Answer (B)
Total expenditure (in Rs crores) = 48
% expenditure of the company Q, R and T together = (22+18+20) = 60%
=> Total expenditure (in Rs crores) of the company Q, R and T together = $\frac{60}{100}\times48$
= $\frac{144}{5}=28.8$
=> Ans – (B)