LR Questions for CAT [PDF]

The CAT has moved away from the traditional DILR sets, it’s imperative to practice the non-traditional type of sets. The sets that are appearing are more logic-based. You can check out the CAT LR questions based on CAT Previous year’s papers. In this article, we will provide you with LR questions for CAT with solutions PDF which is very important to prepare for the CAT exam. These are good sources for practising including logical reasoning questions and answers. Click on the below link to download the PDF

Download LR Questions for CAT

Enroll for CAT 2022 Online Course

Instructions

A significant amount of traffic flows from point S to point T in the one-way street network shown below. Points A, B, C, and D are junctions in the network, and the arrows mark the direction of traffic flow. The fuel cost in rupees for travelling along a street is indicated by the number adjacent to the arrow representing the street. –

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI-2.png”/>

Motorists traveling from point S to point T would obviously take the route for which the total cost of traveling is the minimum. If two or more routes have the same least travel cost, then motorists are indifferent between them. Hence, the traffic gets evenly distributed among all the least cost routes.

The government can control the flow of traffic only by levying appropriate toll at each junction. For example, if a motorist takes the route S-A-T (using junction A alone), then the total cost of travel would be Rs 14 (i.e., Rs 9 + Rs 5) plus the toll charged at junction A.

Question 1: If the government wants to ensure that all motorists travelling from S to T pay the same amount (fuel costs and toll combined) regardless of the route they choose and the street from B to C is under repairs (and hence unusable), then a feasible set of toll charged (in rupees) at junctions A, B, C, and D respectively to achieve this goal is:

a) 2,5,3,2

b) 0,5,3,2

c) 1,5,3,2

d) 2,3,5,1

e) 1,3,5,1

1) Answer (C)

View Video Solution

Solution:

Let the toll charged at junctions A, B, C, and D be a,b,c and d respectively. Then the so that equal amount is collected through all route we have, 9+a+5=2+b+2+a+5=10+d+c=13+d. Then from the options only option C satisfies the above equality. hence option C.

Question 2: If the government wants to ensure that no traffic flows on the street from D to T, while equal amount of traffic flows through junctions A and C, then a feasible set of toll charged (in rupees) at junctions A, B, C,and D respectively to achieve this goal is:

a) 1,5,3,3

b) 1,4,4,3

c) 1,5,4,2

d) 0,5,2,3

e) 0,5,2,2

2) Answer (E)

View Video Solution

Solution:

Let the toll charged at junctions A, B, C, and D be a,b,c and d respectively. Now since we want equal traffic through A and C , total cost through routes passing from A and C should be equal. So we have (9+a+5) + (2+b+2+a+5) = (2+3+b+c+2) + (7+d+1+c+2) . Only option E satisfy the above equality.

Question 3: If the government wants to ensure that all routes from S to T get the same amount of traffic, then a feasible set of toll charged (in rupees) at junctions A, B, C, and D respectively to achieve this goal is:

a) 0, 5, 2, 2

b) 0,5,4,1

c) 1,5,3,3

d) 1, 5, 3,2

e) 1,5,4,2

3) Answer (D)

View Video Solution

Solution:

Now  the fuel cost along different routes are :
SAT = 14
SBAT = 9
SBCT = 7
SDCT = 10
SDT = 13
Now , if we consider option D . Total cost for all routes comes out to be same which is 15. Hence option D.

Question 4: If the government wants to ensure that the traffic at S gets evenly distributed along streets from S to A, from S to B, and from S to D, then a feasible set of toll charged (in rupees) at junctions A, B, C, and D respectively to achieve this goal is:

a) 0,5,4,1

b) 0,5,2,2

c) 1,5,3,3

d) 1,5,3,2

e) 0,4,3,2

4) Answer (A)

View Video Solution

Solution:

Total cost = fuel cost + toll
Total cost along SAT : 14+tollA
Total cost along SBAT : 9+tollA+tollB
Total cost along SDT : 13+tollD
Now when option A is considered , total costs come out to be same.
​Hence option A is correct.

Question 5: The government wants to devise a toll policy such that the total cost to the commuters per trip is minimized. The policy should also ensure that not more than 70 per cent of the total traffic passes through junction B. The cost incurred by the commuter travelling from point S to point T under this policy will be:

a) Rs 7

b) Rs 9

c) Rs 10

d) Rs 13

e) Rs 14

5) Answer (C)

View Video Solution

Solution:

The costs of the routes are as given below:
S – B – C – T = 7
S – B – A – T = 9
S – D – C – T = 10
S – D – T = 13
S – A -T = 14
Hence now 100% of the traffic flows through S – B – C – T
Now if we make the cost of traveling through S – B – C – T same as some other route not going through B, then the traffic will be equally distributed between these two routes. The lowest such route is S-D-C-T. The difference in cost = 3. Hence if we levy a toll of Rs.3 at B, the costs of SBCT and SBAT become 10,12 respectively and other routes are not affected. So 50% traffic flows through SBCT and 50% flows through SDCT . Hence cost in this policy = 10.

Instructions

Mathematicians are assigned a number called Erdos number (named after the famous mathematician, Paul Erdos). Only Paul Erdos himself has an Erdos number of zero. Any mathematician who has written a research paper with Erdos has an Erdos number of 1.For other mathematicians, the calculation of his/her Erdos number is illustrated below:

Suppose that a mathematician X has co-authored papers with several other mathematicians. ‘From among them, mathematician Y has the smallest Erdos number. Let the Erdos number of Y be y. Then X has an Erdos number of y+1. Hence any mathematician with no co-authorship chain connected to Erdos has an Erdos number of infinity. :

In a seven day long mini-conference organized in memory of Paul Erdos, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdos number. Nobody had an Erdos number less than that of F.

On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdos number of the group of eight mathematicians to 3. The Erdos numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdos number of the group of eight to as low as 3.

• At the end of the third day, five members of this group had identical Erdos numbers while the other three had Erdos numbers distinct from each other.

• On the fifth day, E co-authored a paper with F which reduced the group’s average Erdos number by 0.5. The Erdos numbers of the remaining six were unchanged with the writing of this paper.

• No other paper was written during the conference.

Question 6: How many participants in the conference did not change their Erdos number during the conference?

a) 2

b) 3

c) 4

d) 5

e) Cannot be determined

6) Answer (D)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

So B,D ,F,G,H are 5 participants in the conference who did not change their Erdos number during the conference.

Question 7: The Erdos number of C at the end of the conference was:

a) 1

b) 2

c) 3

d) 4

e) 5

7) Answer (B)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Erdos no. of C at the end is f+1 = 1+1 = 2. Hence option B.

Question 8: The Erdos number of E at the beginning of the conference was:

a) 2

b) 5

c) 6

d) 7

e) 8

8) Answer (C)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence erdos no. of E at the beginning of conference would be f+5 = 6 .

Question 9: How many participants had the same Erdos number at the beginning of the conference?

a) 2

b) 3

c) 4

d) 5

e) Cannot be determined

9) Answer (B)

View Video Solution

Solution:

Since at the end of the 3rd day 5 people had identical erdos no.(f+1) so : 5*(f+1) +f+f+5+x = 24 ; Only f=1 and x = 7 satisfies the equation. So out of 5 people who had identical erdos no. at the end of day 3, 2 of them had different nos. at the beginning. So there were 5-2 = 3 participants who had the same Erdos number at the beginning of the conference.

Question 10: The person having the largest Erdos number at the end of the conference must have had Erdos number (at that time):

a) 5

b) 7

c) 9

d) 14

e) 15

10) Answer (B)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20

So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5,one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence the person having the largest Erdos number at the end of the conference must have had Erdos number 7 . Hence option B.

Checkout: CAT Free Practice Questions and Videos

Instructions

DIRECTIONS for the following three questions: Answer the questions on the basis of the information given below.

Five friends meet every morning at Sree Sagar restaurant for an idli-vada breakfast. Each consumes a different number of idlis and vadas. The number of idlis consumed are 1, 4, 5, 6, and 8, while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.

i. The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis.

ii. Three persons, including the one who eats four vadas eat without chutney.

iii. Sandeep does not take any chutney.

iv. The one who eats one idli a day does not eat any vadas or chutney. Further, he is not Mukesh.

v. Daljit eats idli with chutney and also eats vada.

vi. Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does.

vii. Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal.

Question 11: Which one of the following statements is true?

a) Daljit eats 5 idlis

b) Ignesh eats 8 idlis

c) Bimal eats 1 idli.

d) Bimal eats 6 idlis.

11) Answer (A)

View Video Solution

Solution:

Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

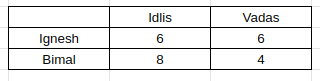
Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

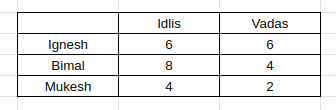
Daljit also eats Vada as per info (v), so we get the following

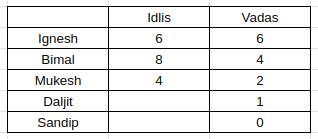
(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

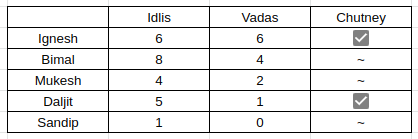
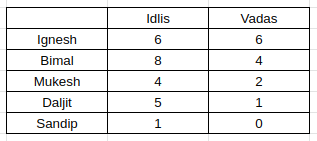
Option A, stating that Daljit eats 5 idlis, is right.

Question 12: Which of the following statements is true?

a) Sandeep eats 2 vadas.

b) Mukesh eats 4 vadas.

c) Ignesh eats 6 vadas.

d) Bimal eats 2 vadas.

12) Answer (C)

View Video Solution

Solution:

Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eats 6 Vadas.

Question 13: Which of the following statements is true?

a) Mukesh eats 8 idlis and 4 vadas but no chutney.

b) The person who eats 5 idlis and 1 vada does not take chutney.

c) The person who eats equal number of vadas and idlis also takes chutney.

d) The person who eats 4 idlis and 2 vadas also takes chutney.

13) Answer (C)

View Video Solution

Solution:

Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eating 6 vadas and 6 idlis eat Chutney.

Instructions

A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.

Question 14: The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
How many different sequences of scans are allowed for any given person’s original scan?

14) Answer: 11

View Video Solution

Solution:

Let the original sequence be TIMRL

Two fingers can be out of place. This can be done if and only if two fingers interchange their position. These two can be selected in $^5C_2 = 10$ ways. In addition to these, the original sequence will also be accepted. Hence the total number of acceptable sequences = 10 + 1 = 11

Question 15: The lab has decided to allow variations of the original sequence so that input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. Thus, for example, if TIMRL is the original sequence, then ITRML is also allowed, but LIMRT is not.
How many different sequences are allowed for any given person’s original scan?

a) 7

b) 5

c) 8

d) 13

15) Answer (C)

View Video Solution

Solution:

Input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. This can be achieved only when two consecutive fingers are interchanged. Let the original sequence be TIMRL
Case 1: Only a set of two consecutive numbers are interchanged.
They can be selected in 5-1 = 4 ways
Case 2: Two sets of two consecutive numbers are interchanged.
(i) TI are interchanged, => (MR, RL) => 2 ways
(ii) IM are interchanged => (RL) => 1 way
Total no of ways possible = 4 + 2 + 1 = 7

Including the original sequence, we get the total number of allowed combinations as 8

Checkout: CAT Free Practice Questions and Videos

Question 16: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) where at most two scans (out of six) are out of place, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed for any given person’s original scan?

16) Answer: 15

View Video Solution

Solution:

There can be two scans out of place.

TIMTRL is the original sequence.

If T is interchanged: There will be four ways: ITMTRL, MITTRL, RIMTTL, LIMTRT

If I is interchanged: There will be four ways

If M is interchanged: There will be three ways

If T is interchanged: There will be two ways

If R is interchanged: There will be one way

Total 14.

Another sequence allowed is original, So total 15 ways.

Question 17: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) so that input in the form of scanned sequence of six fingers is allowed to vary from the original sequence by one place for any of the fingers, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed if the original scan sequence is LRLTIM?

a) 8

b) 11

c) 13

d) 14

17) Answer (C)

View Video Solution

Solution:

1. If original sequence is given.

2. If either of LR, RL, LT, TI, IM is interchanged => 5 ways.

3. If LR and LT and IM interchanged. The sequence will look like: RLTLMI

4. If LR and LT are interchanged.

5. If LR and TI are interchanged.

6. If LR and IM are interchanged.

7. If RL and TI are interchanged.

8. If RL and IM  are interchanged.

9. If LT and IM are interchanged.

Total 13 ways possible.

Instructions

Directions for the following three questions: Answer the questions based on the pipeline diagram below.

The following sketch shows the pipelines carrying material from one location to another. Each location has a demand for material. The demand at Vaishali is 400, at Jyotishmati is 400, at Panchal is 700, and at Vidisha is 200. Each arrow indicates the direction of material flow through the pipeline. The flow from Vaishali to Jyotishmati is 300. The quantity of material flow is such that the demands at all these locations are exactly met. The capacity of each pipeline is 1,000.

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_5_1.png”/>

Question 18: The quantity moved from Avanti to Vidisha is

a) 200

b) 800

c) 700

d) 1,000

18) Answer (D)

View Video Solution

Solution:

We know that quantity between Vaishali and jyotishmati is 300,

So quantity in avanti-vaishal route should be 700.

Now at jyotishmati the required quantity is 400+700 = 1100.

But through vaishali only 300 comes , so  800 should come through Vidisha-jyotishmati route.

Now demand at vidisha is 200. So total quantity required in avanti – vidisha route is 800+200=1000. Hence option D.

Question 19: The free capacity available at the Avanti-Vaishali pipeline is

a) 0

b) 100

c) 200

d) 300

19) Answer (D)

View Video Solution

Solution:

We know that quantity between Vaishali and jyotishmati is 300,

So quantity in avanti-vaishal route should be 400+300=700.

So free capacity is 1000-700=300. Hence option D .

Question 20: What is the free capacity available in the Avanti-Vidisha pipeline?

a) 300

b) 200

c) 100

d) 0

20) Answer (D)

View Video Solution

Solution:

We know that quantity between Vaishali and jyotishmati is 300, So quantity in avanti-vaishal route should be 700. Now at jyotishmati the required quantity is 400+700 = 1100.

But through vaishali only 300 comes , so  800 should come through Vidisha-jyotishmati route.

Now demand at vidisha is 200. So total quantity required in avanti – vidisha route is 800+200=1000.

Hence, free capacity available = 1000-1000=0. Hence option D.

Enroll to CAT 2022 Online Coaching

Download CAT Quant Formulas PDF