Logical Reasoning Questions for CAT have appeared in the CAT Quant section. You can check out the CAT Logical Reasoning questions based on CAT Previous year’s papers. In this article, we will look into some important Logical Reasoning questions for CAT with solutions PDF. These are good sources for practice.
To ace this section, the only trick is to practice different types of questions which are tricky. Here in this PDF most of the questions are tricky logical reasoning questions with answers. So, you can utilize this PDF for practising.
Click on the below link to download the CAT logical reasoning questions and answers pdf
Download Logical Reasoning Questions for CAT
Enroll for CAT 2022 Online Course
Instructions
DIRECTIONS for the following three questions: Answer the questions on the basis of the information given below.
Five friends meet every morning at Sree Sagar restaurant for an idli-vada breakfast. Each consumes a different number of idlis and vadas. The number of idlis consumed are 1, 4, 5, 6, and 8, while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.
i. The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis.
ii. Three persons, including the one who eats four vadas eat without chutney.
iii. Sandeep does not take any chutney.
iv. The one who eats one idli a day does not eat any vadas or chutney. Further, he is not Mukesh.
v. Daljit eats idli with chutney and also eats vada.
vi. Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does.
vii. Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal.
Question 1: Which one of the following statements is true?
a) Daljit eats 5 idlis
b) Ignesh eats 8 idlis
c) Bimal eats 1 idli.
d) Bimal eats 6 idlis.
1) Answer (A)
Solution:
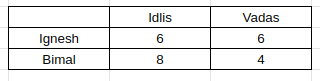
Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.
Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.
Using (vii), Bimal eats 2 more idlis than Ignesh.
Possibilities:
Bimal – 8, Ignesh – 6
Bimal – 6, Ignesh – 4
But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.
Hence we take Bimal – 8 and Ignesh – 6.
Also, we get that Bimal eats 6 – 2 = 4 vadas.
So far, we get the following information.
Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.
So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get
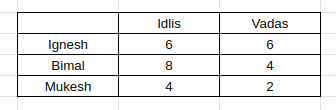
Daljit also eats Vada as per info (v), so we get the following
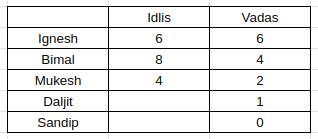
(iv) gives us the information that the one who eats 1idli does not have vada.
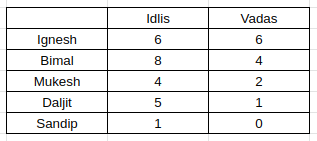
Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).
Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.
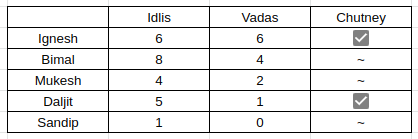
Option A, stating that Daljit eats 5 idlis, is right.
Question 2: Which of the following statements is true?
a) Sandeep eats 2 vadas.
b) Mukesh eats 4 vadas.
c) Ignesh eats 6 vadas.
d) Bimal eats 2 vadas.
2) Answer (C)
Solution:
Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.
Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.
Using (vii), Bimal eats 2 more idlis than Ignesh.
Possibilities:
Bimal – 8, Ignesh – 6
Bimal – 6, Ignesh – 4
But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.
Hence we take Bimal – 8 and Ignesh – 6.
Also, we get that Bimal eats 6 – 2 = 4 vadas.
So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.
So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).
Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eats 6 Vadas.
Question 3: Which of the following statements is true?
a) Mukesh eats 8 idlis and 4 vadas but no chutney.
b) The person who eats 5 idlis and 1 vada does not take chutney.
c) The person who eats equal number of vadas and idlis also takes chutney.
d) The person who eats 4 idlis and 2 vadas also takes chutney.
3) Answer (C)
Solution:
Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.
Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.
Using (vii), Bimal eats 2 more idlis than Ignesh.
Possibilities:
Bimal – 8, Ignesh – 6
Bimal – 6, Ignesh – 4
But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.
Hence we take Bimal – 8 and Ignesh – 6.
Also, we get that Bimal eats 6 – 2 = 4 vadas.
So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.
So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).
Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eating 6 vadas and 6 idlis eat Chutney.
Instructions
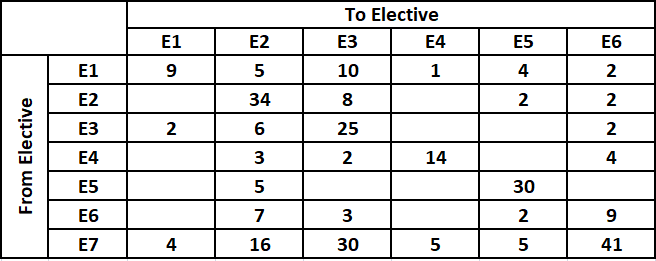
There were seven elective courses – E1 to E7 – running in a specific term in a college. Each of the 300 students enrolled had chosen just one elective from among these seven. However, before the start of the term, E7 was withdrawn as the instructor concerned had left the college. The students who had opted for E7 were allowed to join any of the remaining electives. Also, the students who had chosen other electives were given one chance to change their choice. The table below captures the movement of the students from one elective to another during this process. Movement from one elective to the same elective simply means no movement. Some numbers in the table got accidentally erased; however, it is known that these were either 0 or 1.
Further, the following are known:
1. Before the change process there were 6 more students in E1 than in E4, but after the reshuffle, the number of students in E4 was 3 more than that in E1.
2. The number of students in E2 increased by 30 after the change process.
3. Before the change process, E4 had 2 more students than E6, while E2 had 10 more students than E3.
Question 4: How many elective courses among E1 to E6 had a decrease in their enrollments after the change process?
a) 4
b) 1
c) 2
d) 3
4) Answer (C)
Solution:
From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.
It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.
It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.
Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle = 9 + 5 + 10 + 1 + 4 + 2 = 31.
It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.
Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle = 25 – 2 = 23.
All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.
Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.
Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.
For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.
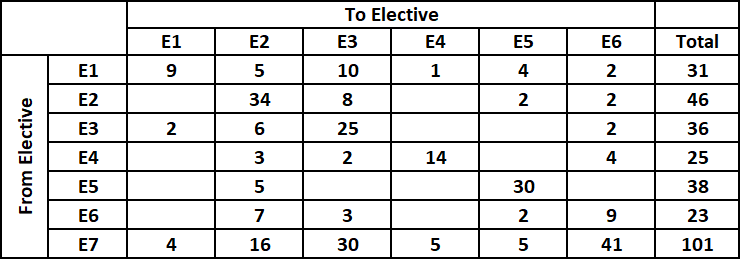
For elective E2,
Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 0
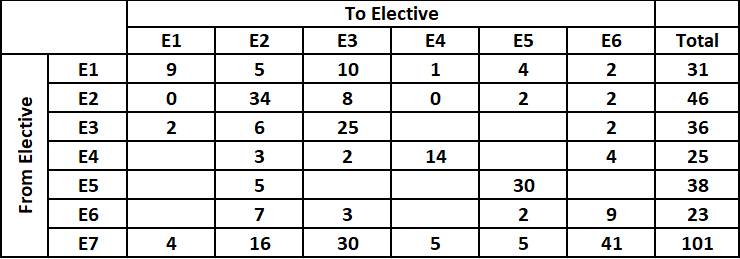
For elective E4,
Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25
i.e. Number of students who moved from to E1 = Number of students who moved from to E5 = 1 {As the remaining blanks can be filled by either 0 or 1}
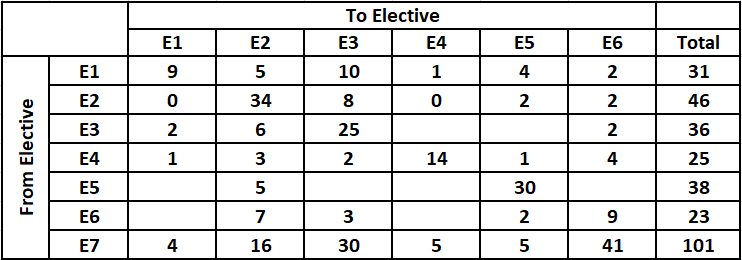
For elective E6,
Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 1 {As the remaining blanks can be filled by either 0 or 1}
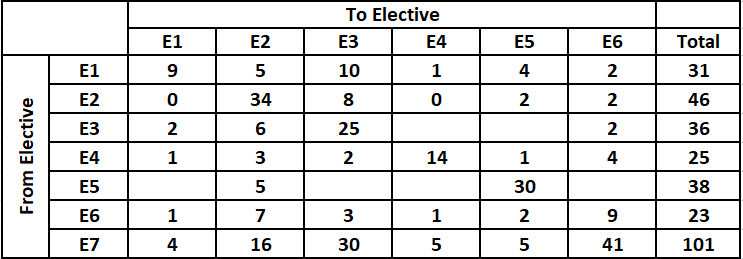
It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 + E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}
Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4 = 17 + E5 to E1.
Hence, it is possible only when E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.
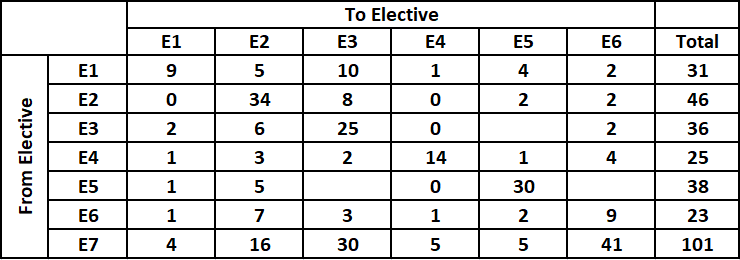
Remaining blank places can be filled easily as we know the total sum of each row.
Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

Form the table we can see that the number of students who enrolled for E1 and E4 decreased from 31 and 25 to 18 and 21 respectively.
Therefore, option C is the correct answer.
Question 5: After the change process, which of the following is the correct sequence of number of students in the six electives E 1 to E6?
a) 19, 76, 79, 21, 45, 60
b) 19, 76, 78, 22, 45, 60
c) 18, 76, 79, 23, 43, 61
d) 18, 76, 79, 21, 45, 61
5) Answer (D)
Solution:
From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.
It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.
It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.
Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle = 9 + 5 + 10 + 1 + 4 + 2 = 31.
It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.
Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle = 25 – 2 = 23.
All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.
Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.
Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.
For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,
Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 0

For elective E4,
Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25
i.e. Number of students who moved from to E1 = Number of students who moved from to E5 = 1 {As the remaining blanks can be filled by either 0 or 1}

For elective E6,
Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 1 {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 + E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}
Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4 = 17 + E5 to E1.
Hence, it is possible only when E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.
Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

Form the table, we can see that after the reshuffle the number of students in electives E1 to E6 are 18, 76, 79, 21, 45 and 61 in that order.
Therefore, option D is the correct answer.
Question 6: After the change process, which course among E1 to E6 had the largest change in its enrollment as a percentage of its original enrollment?
a) E1
b) E2
c) E3
d) E6
6) Answer (D)
Solution:
From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.
It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.
It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.
Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle = 9 + 5 + 10 + 1 + 4 + 2 = 31.
It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.
Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle = 25 – 2 = 23.
All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.
Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.
Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.
For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,
Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 0

For elective E4,
Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25
i.e. Number of students who moved from to E1 = Number of students who moved from to E5 = 1 {As the remaining blanks can be filled by either 0 or 1}

For elective E6,
Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 1 {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 + E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}
Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4 = 17 + E5 to E1.
Hence, it is possible only when E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.
Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

We are asked the largest change in its enrollment as a percentage of its original enrollment for all 6 electives but as we can see there are only 4 electives. Hence, we will check only for E1, E2, E3 and E6.
The percentage change in the number of students for E1 = $\dfrac{18-31}{31}\times 100$ $\approx$ 42 %
The percentage change in the number of students for E2 = $\dfrac{76-46}{46}\times 100$ $\approx$ 65 %
The percentage change in the number of students for E3 = $\dfrac{79-36}{36}\times 100$ $\approx$ 119 %
The percentage change in the number of students for E6 = $\dfrac{61-23}{23}\times 100$ $\approx$ 165 %
We can see that the percent change in the number of student for E6 is the largest. Therefore, option D is the correct answer.
Question 7: Later, the college imposed a condition that if after the change of electives, the enrollment in any elective (other than E7) dropped to less than 20 students, all the students who had left that course will be required to re-enroll for that elective.
Which of the following is a correct sequence of electives in decreasing order of their final enrollments?
a) E2, E3, E6, E5, E1, E4
b) E3, E2, E6, E5, E4, E1
c) E2, E5, E3, E1, E4, E6
d) E2, E3, E5, E6, E1, E3
7) Answer (A)
Solution:
From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.
It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.
It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.
Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle = 9 + 5 + 10 + 1 + 4 + 2 = 31.
It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.
Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle = 25 – 2 = 23.
All the students from E7 moved to one of electives among E1 to E6. Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.
Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.
Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.
For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,
Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 0

For elective E4,
Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25
i.e. Number of students who moved from to E1 = Number of students who moved from to E5 = 1 {As the remaining blanks can be filled by either 0 or 1}

For elective E6,
Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23
i.e. Number of students who moved from to E1 = Number of students who moved from to E4 = 1 {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1. As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 + E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}
Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4 = 17 + E5 to E1.
Hence, it is possible only when E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.
Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

We can see from the table that number of students enrolled in E1 dropped to 18. Hence, all the students who moved from E1 to any other elective will have to re-enroll in E1.
We can see that the number of students who enrolled for E1 prior to reshuffle = 31. Out of these 31 students, 9 students didn’t move to any other elective whereas remaining 22 students moved to other electives. Hence, all these 22 students have to re-enroll in E1.
Therefore, the total number of students in E1 post re-enrollment = 18 + 22 = 40 which is shown in the table.
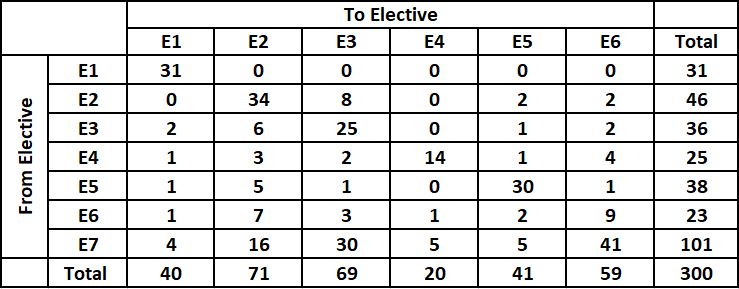
Therefore, the sequence of electives in decreasing order of their final enrollments = E2, E3, E6, E5, E1, E4.
Hence, option A is the correct answer.
Instructions
At a management school, the oldest M dorms, numbered 1 to 10, need to be repaired urgently. This following diagram represents the estimated repair costs (in Rs. Crores for, the 10 dorms. For any dorm, the estimated repair cost (in Rs. Crores ) is an integer. Repairs with estimated cost Rs. 1 or 2 Crores are considered light repairs, repairs with estimated cost Rs. 3 or 4 are considered moderate repairs and repairs with estimated cost Rs. 5 or 6 Crores are considered extensive repairs.
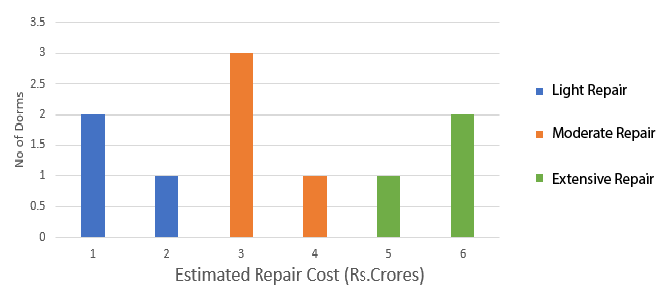
Further, the following information is known.
1. Odd-numbered dorms do not need light repair; even-numbered dorms do not need moderate repair and dorms, whose numbers are divisible by 3, do not need extensive repair.
2. Dorms 4 to 9 all need different repair costs, with Dorm 7 needing the maximum and Dorm 8 needing the minimum.
Question 8: Which of the following is NOT necessarily true?
a) Dorm 1 needs a moderate repair
b) Dorm 5 repair will cost no more than Rs. 4 Crores
c) Dorm 7 needs an extensive repair
d) Dorm 10 repair will cost no more than Rs. 4 Crores
8) Answer (D)
Solution:
Odd numbered dorms need either moderate or extensive repair.
Even numbered dorms need either light or extensive repair.
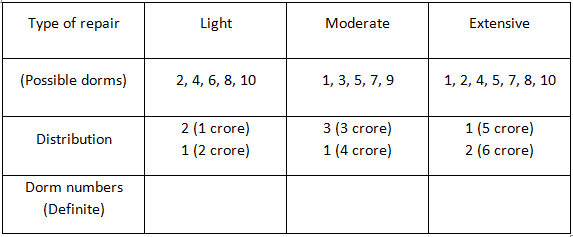
It has been given that dorms 4 to 9 all require different repairing costs. The dorms 3 and 9 should require moderate repair (going by the table). Dorm 7 costs the highest. Therefore, dorm 7 should require 6 crores to repair. Dorm 8 requires the least cost to repair. Therefore, dorm 8 should cost 1 crore to repair. We can eliminate these dorm numbers from other 2 lists.
.png)
Dorms 4 to 9 cost different costs to repair. => Both dorms 5 and 9 cannot require the same cost of repair. Dorms 1 and 3 should require 3 crores to repair.
Dorm 6 should require light repair (2 crores) since dorm 8 requires 1 crore to repair.
=> Dorm 4 requires 5 crore to repair.

We can see that all options except option D are definitely true. Option D cannot be ascertained to be true. Dorm 10 can cost Rs. 1 crore or Rs. 6 crores to repair. Therefore, option D is the right answer.
Question 9: What is the total cost of repairing the odd-numbered dorms (in Rs. Crores)?
9) Answer: 19
Solution:
Odd numbered dorms need either moderate or extensive repair.
Even numbered dorms need either light or extensive repair.

It has been given that dorms 4 to 9 all require different repairing costs. The dorms 3 and 9 should require moderate repair (going by the table). Dorm 7 costs the highest. Therefore, dorm 7 should require 6 crores to repair. Dorm 8 requires the least cost to repair. Therefore, dorm 8 should cost 1 crore to repair. We can eliminate these dorm numbers from other 2 lists.
.png)
Dorms 4 to 9 cost different costs to repair. => Both dorms 5 and 9 cannot require the same cost of repair. Dorms 1 and 3 should require 3 crores to repair.
Dorm 6 should require light repair (2 crores) since dorm 8 requires 1 crore to repair.
=> Dorm 4 requires 5 crore to repair.

Cost = 3 + 3 + 6 + 3 + 4 = Rs.19 crores. Therefore, 19 is the correct answer.
Question 10: Suppose further that:
1. 4 of the 10 dorms needing repair are women’s dorms and need a total of Rs. 20 Crores for repair.
2. Only one of Dorms 1 to 5 is a women’s dorm.
What is the cost for repairing Dorm 9 (in Rs. Crores)?
10) Answer: 3
Solution:
Odd numbered dorms need either moderate or extensive repair.
Even numbered dorms need either light or extensive repair.

It has been given that dorms 4 to 9 all require different repairing costs. The dorms 3 and 9 should require moderate repair (going by the table). Dorm 7 costs the highest. Therefore, dorm 7 should require 6 crores to repair. Dorm 8 requires the least cost to repair. Therefore, dorm 8 should cost 1 crore to repair. We can eliminate these dorm numbers from other 2 lists.
.png)
Dorms 4 to 9 cost different costs to repair. => Both dorms 5 and 9 cannot require the same cost of repair. Dorms 1 and 3 should require 3 crores to repair.
Dorm 6 should require light repair (2 crores) since dorm 8 requires 1 crore to repair.
=> Dorm 4 requires 5 crore to repair.

There are 3 dorms from 6 to 10 which are women’s dorms.
It has been given that the cost of repairing the woman dorms add up to 20. Therefore, the distribution of the costs should be 6+6+5+3.
Dorm 4 is the dorm whose number is below 5 but is a woman’s dorm. Therefore, dorm 9 should cost Rs.3 crores to repair. Dorm 8 cannot be a woman’s dorm. Therefore, dorm 10 should be a woman’s dorm and should cost Rs. 6 crore to repair.
Dorm 9 will cost Rs.9 crore to repair and hence, 9 is the correct answer.
Checkout: CAT Free Practice Questions and Videos
Instructions
A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.
Question 11: The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
How many different sequences of scans are allowed for any given person’s original scan?
11) Answer: 11
Solution:
Let the original sequence be TIMRL
Two fingers can be out of place. This can be done if and only if two fingers interchange their position. These two can be selected in $^5C_2 = 10$ ways. In addition to these, the original sequence will also be accepted. Hence the total number of acceptable sequences = 10 + 1 = 11
Question 12: The lab has decided to allow variations of the original sequence so that input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. Thus, for example, if TIMRL is the original sequence, then ITRML is also allowed, but LIMRT is not.
How many different sequences are allowed for any given person’s original scan?
a) 7
b) 5
c) 8
d) 13
12) Answer (C)
Solution:
Input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. This can be achieved only when two consecutive fingers are interchanged. Let the original sequence be TIMRL
Case 1: Only a set of two consecutive numbers are interchanged.
They can be selected in 5-1 = 4 ways
Case 2: Two sets of two consecutive numbers are interchanged.
(i) TI are interchanged, => (MR, RL) => 2 ways
(ii) IM are interchanged => (RL) => 1 way
Total no of ways possible = 4 + 2 + 1 = 7
Including the original sequence, we get the total number of allowed combinations as 8
Question 13: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) where at most two scans (out of six) are out of place, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed for any given person’s original scan?
13) Answer: 15
Solution:
There can be two scans out of place.
TIMTRL is the original sequence.
If T is interchanged: There will be four ways: ITMTRL, MITTRL, RIMTTL, LIMTRT
If I is interchanged: There will be four ways
If M is interchanged: There will be three ways
If T is interchanged: There will be two ways
If R is interchanged: There will be one way
Total 14.
Another sequence allowed is original, So total 15 ways.
Question 14: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) so that input in the form of scanned sequence of six fingers is allowed to vary from the original sequence by one place for any of the fingers, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed if the original scan sequence is LRLTIM?
a) 8
b) 11
c) 13
d) 14
14) Answer (C)
Solution:
1. If original sequence is given.
2. If either of LR, RL, LT, TI, IM is interchanged => 5 ways.
3. If LR and LT and IM interchanged. The sequence will look like: RLTLMI
4. If LR and LT are interchanged.
5. If LR and TI are interchanged.
6. If LR and IM are interchanged.
7. If RL and TI are interchanged.
8. If RL and IM are interchanged.
9. If LT and IM are interchanged.
Total 13 ways possible.
Instructions
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Question 15: In which of the following years were there two or more contracts?
a) 2017
b) 2016
c) 2015
d) 2018
15) Answer (C)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From
I, Z has at least one contract every year, the only possible
combination is 7+3 or 7+4 year contract and that 7-year contract must be
from B.
From III, Vendor W had contracts only in 2012 and
from VII, Institutes B and D each had exactly one contract in 2012
=> W has got contracts from A and C.
From II. Vendor X had one
or more contracts in every year up to 2015, but no contract in any year
after that and from VI, VII: C and D didn’t have any contract in 2011
and 2010 respectively => A should have X as a 3-year contract from
2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must
have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X
has D for a 4-year contract from 2012-2015 and C must have Z for a
three-year contract in the period 2017-2019 such that Z has at least
one contract every year.
It is known that over the decade, the
institutes each got into two contracts with two of these vendors, and
each vendor got into two contracts with two of these institutes => A
hasn’t got any contract from 2013-2019 as it has X, W in the period
2010-2012 and similarly, C shouldn’t have any contracts in the years 2010,
2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in
2010 and 2019 and in 2010 D and C hasn’t got any contract and A has
already got 2 different contracts from two different vendors => Y has
a contract from B in 2010 => B hasn’t got any contracts in 2017,
2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
Out of the given options, only 2015 has two contracts and rest have only one contract in that particular year.
Checkout: CAT Free Practice Questions and Videos
Question 16: Which of the following is true?
a) B had a contract with Z in 2017
b) B had a contract with Y in 2019
c) D had a contract with X in 2011
d) D had a contract with Y in 2019
16) Answer (D)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From I, Z has at least one contract every year, the only possible combination is 7+3 or 7+4 year contract and that 7-year contract must be from B.
From III, Vendor W had contracts only in 2012 and from VII, Institutes B and D each had exactly one contract in 2012 => W has got contracts from A and C.
From II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that and from VI, VII: C and D didn’t have any contract in 2011 and 2010 respectively => A should have X as a 3-year contract from 2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X has D for a 4-year contract from 2012-2015 and C must have Z for a three-year contract in the period 2017-2019 such that Z has at least one contract every year.
It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes => A hasn’t got any contract from 2013-2019 as it has X, W in the period 2010-2012 and similarly, C shouldn’t have any contracts in the years 2010, 2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in 2010 and 2019 and in 2010 D and C hasn’t got any contract and A has already got 2 different contracts from two different vendors => Y has a contract from B in 2010 => B hasn’t got any contracts in 2017, 2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
Option D is true.
Question 17: In how many years during this period was there only one contract?
a) 3
b) 2
c) 4
d) 5
17) Answer (A)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From
I, Z has at least one contract every year, the only possible
combination is 7+3 or 7+4 year contract and that 7-year contract must be
from B.
From III, Vendor W had contracts only in 2012 and
from VII, Institutes B and D each had exactly one contract in 2012
=> W has got contracts from A and C.
From II. Vendor X had one
or more contracts in every year up to 2015, but no contract in any year
after that and from VI, VII: C and D didn’t have any contract in 2011
and 2010 respectively => A should have X as a 3-year contract from
2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must
have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X
has D for a 4-year contract from 2012-2015 and C must have Z for a
three-year contract in the period 2017-2019 such that Z has at least
one contract every year.
It is known that over the decade, the
institutes each got into two contracts with two of these vendors, and
each vendor got into two contracts with two of these institutes => A
hasn’t got any contract from 2013-2019 as it has X, W in the period
2010-2012 and similarly, C shouldn’t have any contracts in the years 2010,
2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in
2010 and 2019 and in 2010 D and C hasn’t got any contract and A has
already got 2 different contracts from two different vendors => Y has
a contract from B in 2010 => B hasn’t got any contracts in 2017,
2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
Only during 2016, 2017 and 2018, there was only one contract.
Question 18: What BEST can be concluded about the number of contracts in 2010?
a) exactly 4
b) exactly 3
c) at least 3
d) at least 4
18) Answer (B)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.
From
I, Z has at least one contract every year, the only possible
combination is 7+3 or 7+4 year contract and that 7-year contract must be
from B.
From III, Vendor W had contracts only in 2012 and
from VII, Institutes B and D each had exactly one contract in 2012
=> W has got contracts from A and C.
From II. Vendor X had one
or more contracts in every year up to 2015, but no contract in any year
after that and from VI, VII: C and D didn’t have any contract in 2011
and 2010 respectively => A should have X as a 3-year contract from
2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must
have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X
has D for a 4-year contract from 2012-2015 and C must have Z for a
three-year contract in the period 2017-2019 such that Z has at least
one contract every year.
It is known that over the decade, the
institutes each got into two contracts with two of these vendors, and
each vendor got into two contracts with two of these institutes => A
hasn’t got any contract from 2013-2019 as it has X, W in the period
2010-2012 and similarly, C shouldn’t have any contracts in the years 2010,
2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in
2010 and 2019 and in 2010 D and C hasn’t got any contract and A has
already got 2 different contracts from two different vendors => Y has
a contract from B in 2010 => B hasn’t got any contracts in 2017,
2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
The Number of contracts in 2010 is three.
Question 19: Which institutes had multiple contracts during the same year?
a) A only
b) B and C only
c) A and B only
d) B only
19) Answer (C)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.\
From
I, Z has at least one contract every year, the only possible
combination is 7+3 or 7+4 year contract and that 7-year contract must be
from B.
From III, Vendor W had contracts only in 2012 and
from VII, Institutes B and D each had exactly one contract in 2012
=> W has got contracts from A and C.
From II. Vendor X had one
or more contracts in every year up to 2015, but no contract in any year
after that and from VI, VII: C and D didn’t have any contract in 2011
and 2010 respectively => A should have X as a 3-year contract from
2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must
have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X
has D for a 4-year contract from 2012-2015 and C must have Z for a
three-year contract in the period 2017-2019 such that Z has at least
one contract every year.
It is known that over the decade, the
institutes each got into two contracts with two of these vendors, and
each vendor got into two contracts with two of these institutes => A
hasn’t got any contract from 2013-2019 as it has X, W in the period
2010-2012 and similarly, C shouldn’t have any contracts in years 2010,
2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in
2010 and 2019 and in 2010 D and C hasn’t got any contract and A has
already got 2 different contracts from two different vendors => Y has
a contract from B in 2010 => B hasn’t got any contracts in 2017,
2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
B and A have multiple contracts in a single year.
Question 20: Which institutes and vendors had more than one contracts in any year?
a) B, W, X, and Z
b) A, B, W, and X
c) A, D, W, and Z
d) B, D, W, and X
20) Answer (B)
Solution:
From IV: A, B, C, D have one 3, 7, 3, 4-year contract respectively and all other contracts are one-year contracts.\
From
I, Z has at least one contract every year, the only possible
combination is 7+3 or 7+4 year contract and that 7-year contract must be
from B.
From III, Vendor W had contracts only in 2012 and
from VII, Institutes B and D each had exactly one contract in 2012
=> W has got contracts from A and C.
From II. Vendor X had one
or more contracts in every year up to 2015, but no contract in any year
after that and from VI, VII: C and D didn’t have any contract in 2011
and 2010 respectively => A should have X as a 3-year contract from
2010-2012. Now, for 2013-2015 X can’t have B for the same. So, X must
have got contracts from either C or D in that period.
Case 1:
X has C as a 3-year contract from 2013-2015 but in this case, D can’t have any contract in 2012 so, this case is not valid.
Case 2:
X
has D for a 4-year contract from 2012-2015 and C must have Z for a
three-year contract in the period 2017-2019 such that Z has at least
one contract every year.
It is known that over the decade, the
institutes each got into two contracts with two of these vendors, and
each vendor got into two contracts with two of these institutes => A
hasn’t got any contract from 2013-2019 as it has X, W in the period
2010-2012 and similarly, C shouldn’t have any contracts in years 2010,
2013, 2014, 2015, 2016.
From III, Vendor Y had contracts in
2010 and 2019 and in 2010 D and C hasn’t got any contract and A has
already got 2 different contracts from two different vendors => Y has
a contract from B in 2010 => B hasn’t got any contracts in 2017,
2018, 2019.
For Y the only possible contract will be from D => D has got no contracts in the years 2011, 2016, 2017, 2018.
Now, the table looks like:

‘N’ represents no contract.
A, B, W, X had more than one contracts in a single year




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
