Hexagon Questions for CAT
Download important CAT Hexagon Questions PDF based on previously asked questions in CAT exam. Practice Hexagon questions with solutions for CAT exam.
Download Hexagon Questions for CAT
Enroll To CAT 3 Months Crash Course
Download CAT Quant Questions PDF
Question 1:
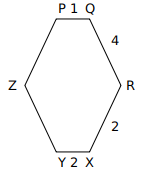
a) 3, 3
b) 4, 2
c) 2, 4
d) 4, 4
Question 2: In the figure below, ABCDEF is a regular hexagon and $\angle{AOF}$ = 90° . FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?
a) 1/12
b) 1/6
c) 1/24
d) 1/18
Download CAT 2019 Syllabus PDF
Question 3: ABCDEF is a regular hexagon and PQR is an equilateral triangle of side a. The area of the shaded portion is X and CD : PQ : : 2 : 1. Find the area of the circle circumscribing the hexagon in terms of X.
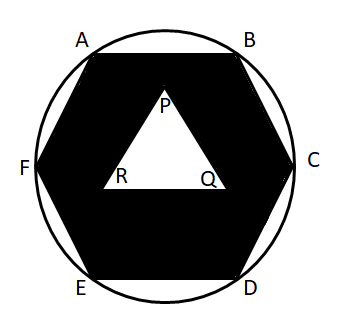
a) $\frac{16 \pi}{23 \sqrt{3}}$ X
b) $\frac{42 \pi}{5 \sqrt{3}}$ X
c) $\frac{2 \pi}{3 \sqrt{3}}$ X
d) $2\sqrt{3 \pi}$ X
Question 4: Let PQRSTU be a regular hexagon. The ratio of the area of the triangle PRT to that of the hexagon PQRSTU is
a) 0.3
b) 0.5
c) 1
d) None of the above
Take a free CAT online mock test
Question 5: Let ABCDEF be a regular hexagon with each side of length 1 cm. The area (in sq cm) of a square with AC as one side is
a) $3\sqrt{2}$
b) $3$
c) $4$
d) $\sqrt{3}$
Answers & Solutions:
1) Answer (A)
Let’s calculate the measure of each internal angle.
Sum of the internal angles of a polygon of n sides = (n-2)*180
Each internal angle =$\frac{(n-2)*180}{n}$
=$120^0$
So the Exterior angle of angle P is $60^0$. APQ forms an equilateral triangle of side 1 cm.
Similarly, RBX forms an equilateral triangle of side 2 cms.
Length of AB =7 cms
ABC is an equilateral triangle of side 7 cms.
Length of CY = length of CB- length of YB
=7-4=3 cms
Length of PZ = Length of AC – (length of AP+ length of CZ)
7-(1+3)
=4 cms
Hence the length of YZ is 3 cms and ZP is 3 cms
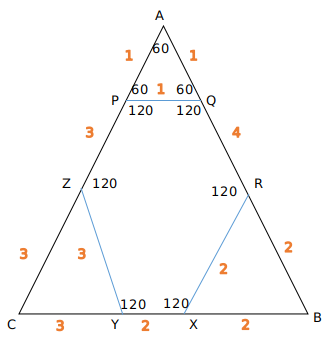
A is the correct answer.
CAT Online Most Trusted Courses
2) Answer (A)
When the hexagon is divided into number of similar triangle AOF we get 12 such triangles . Hence required ratio of area is 1/12.
3) Answer (A)
Let ‘a’ be the length of side of the hexagon. Therefore, the area of hexagon = $6*\dfrac{\sqrt{3}}{4}\times a^2$.
The area of triangle PQR = $\dfrac{\sqrt{3}}{4}\times (a/2)^2$
Therefore, the are of the shaded region = $6*\dfrac{\sqrt{3}}{4}\times a^2$ – $\dfrac{\sqrt{3}}{4}\times (a/2)^2$ = $\dfrac{23\sqrt{3}a^2}{16} = X$
$\Rightarrow$ $a^2 = \dfrac{16X}{23\sqrt{3}}$
The area of the circle = $\pi*a^2$
$\Rightarrow$ $\dfrac{16 \pi}{23 \sqrt{3}}$ X. Hence, option A is the correct answer.
4) Answer (B)
It’s given that PQRSTU is a regular hexagon and O is the center of the hexagon.
If we fold $\triangle$TSR ,$\triangle$PQR ,$\triangle$TUP along lines TR, PR, PT respectively then vertices S,Q,U will overlap each other exactly at center of the hexagon.
Hence we can say that Area of hexagon PQRSTU = 2($\triangle$PRT)
So Area of $\triangle$PRT = 0.5(Area of hexagon PQRSTU)
5) Answer (B)
The length of the diagonals of a regular hexagon with side s are $\sqrt{3}s$.
Here length of AC =
$\sqrt{3}s$ = $\sqrt{3}$ cms
Hence area of the square = $\sqrt{3}^2$ = 3 sq cm
Preparation tips for CAT – Beginners
Download Free CAT Preparation App
We hope this Hexagon questions and answers PDF will be helpful to you.
