Geometry Questions for SSC CGL Tier 2 PDF
Download SSC CGL Tier 2 Geometry Questions PDF. Top 10 SSC CGL Tier 2 Geometry questions based on asked questions in previous exam papers very important for the SSC exam.
Download Geometry Questions for SSC CGL Tier 2 PDF
Get 10 SSC CGL Tier-2 Mocks for Rs. 149
Take SSC CGL Tier-2 Mock Tests
Download SSC CGL Tier-2 Previous Papers PDF
Question 1: If an obtuse-angled triangle ABC, is the obtuse angle and O is the orthocenter. If = 54$^{\circ}$ , then is
a) 108$^{\circ}$
b) 126$^{\circ}$
c) 136$^{\circ}$
d) 116$^{\circ}$
Question 2: BC is the centre of the circle with centre O. A is a point on major arc BC as shown in the above figure. What is the value of $\angle{BAC}+\angle{OBC}$ ?

a) 120$^{\circ}$
b) 60$^{\circ}$
c) 90$^{\circ}$
d) 180$^{\circ}$
Question 3: Internal bisectors of ∠Q and ∠R of ΔPQR intersect at O. If ∠ROQ = 96° then the value of ∠RPQ is
a) 36°
b) 24°
c) 12°
d) 6°
Take SSC CGL Tier-2 Mock Tests
Download SSC CGL Tier-2 Previous Papers PDF
Question 4: In a ΔABC, ∠A+ ∠B = 118° ∠A + ∠C = 96°. find the value of ∠A.
a) 36°
b) 40°
c) 30°
d) 34°
Question 5: In a cyclic quadrilateral ∠A+∠C=∠B+∠D=? 
a) 270°
b) 360°
c) 90°
d) 180°
Question 6: In the given figures, the lengths of the sides of ΔABC and ΔPQR are given and they are given in same units. Also ∠A and ∠B are given. Then value of ∠P is
a) 42°
b) 36°
c) 38°
d) 40°
Question 7: The area of a circle is proportional to the square of its radius. A small circle of radius 3 cm is drawn within a larger circle of radius 5 cm. Find the ratio of the areaof the annular zone to the area of the larger circle. (Area of the annular zone is the difference between the area of the larger circle and that of the smaller circle).
a) 9 : 16
b) 9 : 25
c) 16 : 25
d) 16 : 27
18000+ Questions – Free SSC Study Material
Question 8: In a triangle ABC, AB = AC, LBAC = 40° Then the external angle at B is :
a) 90°
b) 70°
c) 110°
d) 80°
Question 9: If the area of the circle in the figure is 36$\pi$ sq. cm. And ABCD is a square, then the area of $\triangle ACD$, in sq.cm, is
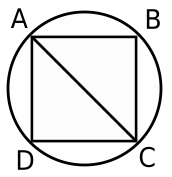
a) $12\pi$
b) $\frac{36}{\pi}$
c) 12
d) None of the above
Question 10: How many balls of radius 3 cm can be made by melting a bigger ball of diameter 48 cm?
a) 1024
b) 512
c) 64
d) 256
Download SSC CGL General Science Notes PDF
Free SSC Preparation (Videos Youtube)
Answers & Solutions:
1) Answer (B)
2) Answer (C)
As we know that angle through an arc on centre is double that of made on remaining arc.
Hence $\angle{BOC}=2\angle{BAC} $=2x (where x=$\angle{BAC} $)
and $\angle{OBC}$ would be 90-x
So $\angle{BAC}+\angle{OBC}$=90
3) Answer (C)
To find : $\angle$RPQ = $\theta$ = ?
Solution : Let $\angle$PQR = $2x$ and $\angle$PRQ = $2y$
=> $\angle$OQR = $x$ and $\angle$ORQ = $y$ [SInce, QO & RO are angle bisectors]
In $\triangle$PQR
=> $\theta$ + $\angle$PQR + $\angle$PRQ = 180°
=> $\theta$ = 180° -2$(x+y)$ ———Eqn(1)
In $\triangle$QOR
=> x + y + 96° = 180°
=> x + y = 84°
Putting value of (x+y) in eqn (1)
=> $\theta$ = 180 – 2*84 = 180-168 = 12°
4) Answer (D)
∠A + ∠B + ∠C = 180
∠A + ∠C = 96°,
∠B= 84, and
from ∠A+ ∠B = 118, ∠A= 34
5) Answer (D)

Sum of opposite angle of cyclic quadrilateral is 180° (D)
6) Answer (D)
as we can see that in the given triangles
$\frac{AB}{RQ} = \frac{AC}{RP} = \frac{CB}{PQ} = \frac{1}{2}$
We know that if ratio of corresponding sides are equal in two triangles ,then the given traingles are similar and in similar triangles ass coressponding angles are also equal.
So , ∠A = ∠R , ∠C = ∠P , ∠B = ∠Q
∠C = 180 – ( 80 + 60) = 40
So ∠P = 40
7) Answer (C)
Area of circle = $\pi r^2$
Area of annular zone = $\pi (5^2 – 3^2) = 16 \pi$ sq. units
Area of larger circle = $\pi * 5^2 = 25 \pi$ sq. units
=> Required ratio = 16 : 25
8) Answer (C)
Since AB = AC => $\angle$ACBC = $\angle$ACB
In $\triangle$ABC
=> $\angle$ABC + $\angle$ACB + $\angle$BAC = 180°
=> 2$\angle$ABC = 180° – 40° = 140°
=> $\angle$ABC = 70°
To find : $\angle$ABD = 180° – $\angle$ABC
= 180° – 70° = 110°
9) Answer (D)
Area of circle = $ \pi \times r^2= 36\pi$ sq.cm
=> $r = \sqrt{36}=6$ cm
=> Diameter of circle = $AC =2r = 12 $ cm
In $\triangle$ ACD, let $AD=CD=s$ cm
=> $(AD)^2+(CD)^2=(AC)^2$
=> $2s^2=(12)^2=144$
=> $s^2=\frac{144}{2}=72$ ———–(i)
$\therefore$ Area of $\triangle$ ACD = $ \frac{1}{2} \times s \times s$
= $\frac{s^2}{2}=36$ $cm^2$
=> Ans – (D)
10) Answer (B)
Since the larger ball is melted, the volume will remain constant.
Radius of big ball = 24 cm and radius of small balls = 3 cm
Let $n$ balls be formed
=> $\frac{4}{3} \times \pi \times 3^3 \times n = \frac{4}{3} \times \pi \times 24^3$
=> $n = \frac{24^3}{3^3} = (\frac{24}{3})^3$
=> $n = 8^3 = 512$
=> Ans – (B)
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Geometry Questions pdf for SSC CGL Tier 2 exam will be highly useful for your Preparation.








