Expected Numerical Ability Questions For IBPS PO PDF

Download important Expected Numerical Ability Questions PDF based on previously asked questions in IBPS PO and other Banking Exams. Practice Expected Numerical Ability Question and Answers for IBPS PO Exam.

Download Expected Numerical Ability Questions For IBPS PO PDF

Instructions

In the following questions two equations numbered I and II are given. You have to solve both the equations and
Give answer a: if x > y
Give answer b: if x ≥ y
Give answer c: if x < y
Give answer d: if x ≤ y
Give answer e: if x = y or the relationship cannot be established.

Question 1: I.  $x^{2}-3x-88=0$
II. $y^{2}+8y-48=0$

a) if x > y

b) if x ≥ y

c) if x < y

d) if x ≤ y

e) if x = y or the relationship cannot be established.

Question 2: I.  $5x^{2}+29x+20=0$
II. $25y^{2}+25y+6=0$

a) if x > y

b) if x ≥ y

c) if x < y

d) if x ≤ y

e) if x = y or the relationship cannot be established.

Question 3: I.  $2x^{2}-11x+12=0$
II. $2y^{2}-19y+44=0$

a) if x > y

b) if x ≥ y

c) if x < y

d) if x ≤ y

e) if x = y or the relationship cannot be established.

IBPS PO Quant Formulas & Shortcuts

IBPS PO Previous papers

Instructions

In the following number series only one number is wrong. Find out the wrong number.

Question 4: 11, 18, 29, 42, 59, 80, 101

a) 42

b) 18

c) 29

d) 59

e) None of these

Question 5: 2, 9, 32, 105, 436, 2195, 13182

a) 436

b) 2195

c) 9

d) 32

e) None of these

Question 6: 5, 55, 495, 3465, 17325, 34650, 51975,

a) 495

b) 34650

c) 55

d) 17325

e) None of these

IBPS PO Free Mock Test

Question 7: 3, 7, 16, 32, 56, 93, 142

a) 56

b) 16

c) 32

d) 7

e) None of these

Question 8: 4, 5, 12, 38, 160, 805, 4836

a) 12

b) 160

c) 38

d) 805

e) None of these

Question 9: $45\% of 300 + \sqrt{?} = 56\% of 750 -10\% of 250$

a) 130

b) 60

c) 260

d) 67600

e) None of these

Question 10: $895 + 440 \div 55 = ?$

a) 456

b) 903

c) 760

d) 45

e) None of these

Question 11: $12 \times 8 + (?)^{2} = (14)^{2}$

a) 10

b) 1000

c) 100

d) 8

e) None of these

Question 12: 48% of 840 = 36% of ?

a) 1080

b) 1320

c) 1240

d) 720

e) None of these

Question 13: $7\frac{1}{6} of 186 + 565 = 2100-?$

a) 222

b) 202

c) 182

d) 172

e) None of these

Question 14: A car runs at the speed of 40 when not serviced and runs at 65 kmph when serviced. After servicing the car covers a certain distance in 5 hours. How much approximate time will the car take to cover the same distance when not serviced ?

a) 10

b) 7

c) 12

d) 8

e) 6

Question 15: If the ages of P and R added to twice the age of Q ,the total becomes 59 .If the age of Q and R are added to thrice age of P,the total becomes 68 and if the age of the P is added to thrice age of Q and thrice the age age of R the total becomes 108 .What is the age of P?

a) 15 years

b) 19 years

c) 17 years

d) 12 years

e) None of these

IBPS PO Previous Papers (Download Pdf)

Question 16: A bag contains 2 red, 3 green and 2 blue balls. 2 balls are to be drawn randomly. What is the probability that the balls drawn contain no blue ball ?

a) 5/7

b) 10/21

c) 2/7

d) 11/21

e) None of these

Question 17: A boat takes 2 hours to travel from point A to B in still water .To find out it’s speed up-stream ,which of the following information is needed.
i. Distance between point A and B
Ii.Time taken to travel down stream from B to A
iii. Speed of the stream of the water
iv. Effective speed of Boat while traveling Downstream from B to A

a) All are required

b) Even these we cannot found the answer

c) Only i,iii, and either ii or iv

d) Only i and iii

e) None of these

Question 18: A and B both start a small business with an investment of Rs. 3500 and Rs. 4000 respectively. At the end of few months from the start of the business, A withdrew from the business completely and B remained for the year. If the annual profit was divided between A and B in the respective ratio of 7 : 12, then after how many months from the start of the business, did A leave the business?

a) Eight

b) Nine

c) Ten

d) Five

e) Seven

Instructions

Study the following graph and answer the following questions
Percentage increase in sale of four commodities A,B,C,D. For the given months.

 

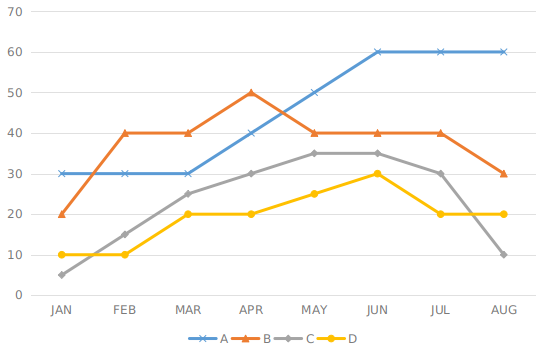
Question 19: For which commodity is percent increase in sale highest in May from January

a) C

b) A

c) B

d) A and B

e) None of these

Question 20: If the sale of C was the 100 in may ,what was its sale in July?

a) 195

b) 100

c) 90

d) cannot be determined

e) None of these

Question 21: In which month(S) did all the commodities showed decline or no increase from the previous Months?

a) Only in July

b) Only in August

c) Only in April and july

d) Only in May ,June ,July.

e) None of these

Question 22: In which month is the average percentage increase for the four commodities the lowest ?

a) May

b) March

c) January

d) June

e) None of these

Question 23: For which months did A show good increase in?

a) Only in April

b) only in May and in August

c) Only in April,june

d) Only in April, May ,June.

e) None of these

Instructions

This data is regarding total number of employees working in Administration (Admin), Operations (Ops.) and other departments of corporate divisions of Companies A and B
The total number of employees working in both the companies together is 4800. The respective ratio of number of employees in Companies A and B is 5 : 7. Each employee works in only one of the mentioned departments.
In company A, 70% of the total employees are males. 60% of the total male employees work in ‘Ops’. Out of the remaining male employees, ${{{1^{th}}} \over 8}$ work in ‘Admin’.
Out of the total female employees, 24% work in ‘Admin’ and$ {{{5^{th}}} \over 8}$ of the remaining female employees work in ‘Ops’.
In company B, 80% of the total employees are males. 65% of the total male employees work in ‘Ops’. Number of male employees who work in ‘other departments’ in Company B is 20% more than the male employees who work in ‘Other departments in company A. Number of female employees who work in Ops in Company B are less than the number of male employees who work for ‘Ops’ in the same company, by 75%. Out of the remaining female employees,$ {1 \over 4} $work in ‘Admin’.

Question 24: What percent of the total number of male employees in company A work in ‘other departments’ ?

a) 45

b) 25

c) 30

d) 35

e) 40

Question 25: What Precent of the total number of female employees in company B work in administration department?

a) 18.5

b) 8.75

c) 14

d) 16

e) 19

Question 26: What is the total number of female employees who work in Ops in Company A and B together?

a) 681

b) 781

c) 689

d) 649

e) 788

Question 27: What is the difference between the average number of males working in ‘Admin’ in both the companies together and average number of females working in ‘Other Departments’ in both the companies together?

a) 26

b) 36

c) 16

d) 24

e) 14

Question 28: In company B, what is the respective ratio between the total number of employees (both male and female) who work in ‘Admin’ and the total number of employees (both male and female) who work in ‘Other department’ in the same company ?

a) 2 : 3

b) 1 : 3

c) 1 : 4

d) 3 : 5

e) 1: 5

Instructions

Refer to the following pie-charts carefully and answer the given questions.

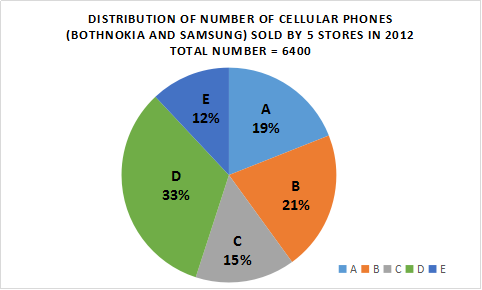
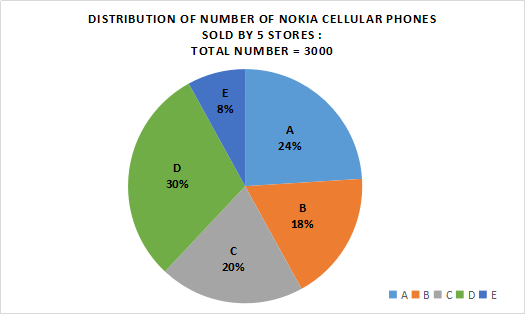
Question 29: Number of cellular phones (both Nokia and Samsung) sold by store B is what percent more than the number of Nokia cellular phones sold by store A?

a) $82{1 \over 3}$

b) $86{2 \over 3}$

c) $84{2 \over 3}$

d) $92{2 \over 3}$

e) $78{1 \over 3}$

Question 30: What is the central angle corresponding to number of cellular phones (both Nokia and Samsung) sold by store D?

a) 124.2°

b) 112.4°

c) 115.2°

d) 120.8°

e) 118.8°

Question 31: What is the average number of Samsung cellular phones sold by stores B, C and D?

a) 796

b) 792

c) 780

d) 812

e) 784

Question 32: What is the difference between number of cellular phones (both Nokia and Samsung) sold by store A and total number of Nokia cellular phones sold by stores B and E together?

a) 442

b) 436

c) 432

d) 428

e) 426

Question 33: Number of Samsung cellular phones sold by store E is what percent of the number of phones (both Nokia and Samsung) sold by store C?

a) 55

b) 45

c) 60

d) 65

e) 50

Instructions

In each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read both the statements and
Give answer
(A) If the data in statement I alone are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question
(B) If the data in statement II alone are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question
(C) If the data either in statement I alone or in statement II alone are sufficient to answer the question
(D) If the data given in both statements I and II together are not sufficient to answer the question and
(E) If the data in both statements I and II together are necessary to answer the question.

Question 34: What is the area of right angle triangle ?
I.Height of right-angled triangle is ¾ th of its base
II.Length of the diagonal of the right angle triangle is 5 meters

a) If the data in statement I alone are sufficient to answer the question, while the data in statement

b) If the data in statement II alone are sufficient to answer the question, while the data in statement

c) If the data either in statement I alone or in statement II alone are sufficient to answer the question

d) If the data given in both statements I and II together are not sufficient to answer the question and

e) If the data in both statements I and II together are necessary to answer the question.

Question 35: What is the present age of the father?
I.Present age of the father five times of the present age of his son
II.5 years ago age of the father is 15 times of the age of his son

a) If the data in statement I alone are sufficient to answer the question, while the data in statement

b) If the data in statement II alone are sufficient to answer the question, while the data in statement

c) If the data either in statement I alone or in statement II alone are sufficient to answer the question

d) If the data given in both statements I and II together are not sufficient to answer the question and

e) If the data in both statements I and II together are necessary to answer the question.

Free IBPS Preparation App

Answers & Solutions:

1) Answer (E)

I.$x^{2} – 3x – 88 = 0$

=> $x^2 + 8x – 11x – 88 = 0$

=> $x (x + 8) – 11 (x + 8) = 0$

=> $(x + 8) (x – 11) = 0$

=> $x = -8 , 11$

II.$y^{2} + 8y – 48 = 0$

=> $y^2 + 12y – 4y – 48 = 0$

=> $y (y + 12) – 4 (y + 12) = 0$

=> $(y + 12) (y – 4) = 0$

=> $y = -12 , 4$

$\therefore$ No relation can be established.

2) Answer (C)

I.$5x^{2} + 29x + 20 = 0$

=> $5x^2 + 25x + 4x + 20 = 0$

=> $5x (x + 5) + 4 (x + 5) = 0$

=> $(x + 5) (5x + 4) = 0$

=> $x = -5 , \frac{-4}{5}$

II.$25y^{2} + 25y + 6 = 0$

=> $25y^2 + 10y + 15y + 6 = 0$

=> $5y (5y + 2) + 3 (5y + 2) = 0$

=> $(5y + 3) (5y + 2) = 0$

=> $y = \frac{-3}{5} , \frac{-2}{5}$

Therefore $x < y$

3) Answer (D)

I.$2x^{2} – 11x + 12 = 0$

=> $2x^2 – 8x – 3x + 12 = 0$

=> $2x (x – 4) – 3 (x – 4) = 0$

=> $(x – 4) (2x – 3) = 0$

=> $x = 4 , \frac{3}{2}$

II.$2y^{2} – 19y + 44 = 0$

=> $2y^2 – 8y – 11y + 44 = 0$

=> $2y (y – 4) – 11 (y – 4) = 0$

=> $(y – 4) (2y – 11) = 0$

=> $y = 4 , \frac{11}{2}$

$\therefore x \leq y$

4) Answer (E)

Prime numbers starting from 7 are added.

11 + 7 = 18

18 + 11 = 29

29 + 13 = 42

42 + 17 = 59

59 + 19 = 78

78 + 23 = 101

Hence, the number which is wrong is 80, as it is not in the options given, the correct answer is None of the above

5) Answer (D)

The pattern followed is :

2 $\times 1 + (1 \times 7)$ = 9

9 $\times 2 + (2 \times 6)$ = 30

30 $\times 3 + (3 \times 5)$ = 105

105 $\times 4 + (4 \times 4)$ = 436

436 $\times 5 + (5 \times 3)$ = 2195

2195 $\times 6 + (6 \times 2)$ = 13182

6) Answer (B)

Consecutive odd numbers starting from 11 in decreasing order are multiplied.

5 $\times 11$ = 55

55 $\times 9$ = 495

495 $\times 7$ = 3465

3465 $\times 5$ = 17325

17325 $\times 3$ = 51975

51975  $\times 1$ = 51975

7) Answer (A)

Squares of natural numbers are added

3 $+ 2^2$ = 7

7 $+ 3^2$ = 16

16 $+ 4^2$ = 32

32 $+ 5^2$ = 57

57 $+ 6^2$ = 93

93 $+ 7^2$ = 142

8) Answer (C)

The pattern followed is :

4 $\times 1 + 1$ = 5

5 $\times 2 + 2$ = 12

12 $\times 3 + 3$ = 39

39 $\times 4 + 4$ = 160

160 $\times 5 + 5$ = 805

805 $\times 6 + 6$ = 4836

9) Answer (D)

Expression : $45\% of 300 + \sqrt{?} = 56\% of 750 -10\% of 250$

=> $(\frac{45}{100} \times 300) + (\sqrt{?}) = (\frac{56}{100} \times 750) – (\frac{10}{100} \times 250)$

=> $135 + \sqrt{?} = 420 – 25$

=> $\sqrt{?} = 395 – 135 = 260$

=> $? = 260^2 = 67600$

10) Answer (B)

Expression : $895 + 440 \div 55 = ?$

= $895 + \frac{440}{55}$

= $895 + 8 = 903$

11) Answer (A)

Expression : $12 \times 8 + (?)^{2} = (14)^{2}$

=> $96 + (?)^2 = 196$

=> $? = \sqrt{196 – 96} = \sqrt{100}$

=> $? = 10$

12) Answer (E)

Expression : 48% of 840 = 36% of ?

=> $\frac{48}{100} * 840 = \frac{36}{100} * ?$

=> $? = \frac{48 \times 840}{36}$

=> $? = 1120$

13) Answer (B)

Expression : $7\frac{1}{6} of 186 + 565 = 2100-?$

=> $(\frac{43}{6} \times 186) + 565 = 2100 – ?$

=> $? = 2100 – 565 – 1333$

=> $? = 202$

14) Answer (D)

After servicing, the distance covered by car in 5 hours = 65 * 5 = 325 km

Without servicing, speed of car = 40 kmph

=> Required time = $\frac{Distance}{Speed}$

= $\frac{325}{40}$ = 8.125 hr

$\approx$ 8 hours

15) Answer (D)

Let ages of P,Q and R be $p,q,r$ respectively

According to ques, => $(p+r)+2q=59$ ————(i)

and $(q+r)+3p=68$ ————-(ii)

and $p+3q+3r=108$ ————(iii)

Multiplying equation (ii) by 3, => $3q+3r+9p = 204$ ———-(iv)

Subtracting equation (iii) from (iv), we get :

=> $(9p-p)=(204-108)$

=> $8p=96$

=> $p=\frac{96}{8}=12$ years

=> Ans – (D)

16) Answer (B)

Total number of balls = 2 + 3 + 2 = 7

Total number of outcomes = Drawing 2 balls out of 7

= $C^7_2 = \frac{7 \times 6}{1 \times 2} = 21$

Favourable outcomes = Drawing 2 balls out of 5 (so that none is blue)

= $C^5_2 = \frac{5 \times 4}{1 \times 2} = 10$

=> Required probability = $\frac{10}{21}$

17) Answer (D)

Time taken by boat to travel from point A to B in still water = 2 hours

To find the upstream speed, we definitely need the speed of stream, thus statement (iii) is mandatory.

Also, the distance between points A and B or the speed of boat in still water is needed.

Thus, statements (i) and (iii) are required to find the upstream speed of the boat.

=> Ans – (D)

18) Answer (A)

Let A remained in the business for $x$ months.

Amount invested by A = Rs. 3500

Amount invested by B = Rs. 4000

Ratio of share in profit received by A and B

=> $\frac{3500 \times x}{4000 \times 12} = \frac{7}{12}$

=> $\frac{7 x}{8 \times 12} = \frac{7}{12}$

=> $x = 8$

$\therefore$ 8 months from the start of the business A left the business.

19) Answer (A)

Percent increase in sale in May from January of commodity :

A = $\frac{50 – 30}{30} \times 100$ = 66.7%

B = $\frac{40 – 20}{20} \times 100$ = 100%

C = $\frac{35 – 5}{5} \times 100$ = 600%    [MAX]

D = $\frac{25 – 10}{10} \times 100$ = 150%

=> Ans – (A)

20) Answer (E)

Sale of C in May = 100

Percent increase in sale of C in June and July = 35% and 30% respectively

=> Sale of C in July = $100 \times \frac{135}{100} \times \frac{130}{100}$

= $135 \times 1.3 = 175.5$

=> Ans – (E)

21) Answer (E)

(A) : In July, A and B neither decline nor increase from previous year, thus it’s not true.

(B) : In August, A and D neither decline nor increase from previous year, thus it’s not true.

(C) : In April,all the commodities increase while in July A and B remained constant, thus it’s not true.

(D) : In May only B show decline, and in June and July none of the commodities declined, thus it’s not true.

=> Ans – (E)

22) Answer (C)

Average percentage increase for the four commodities in :

Jan = $\frac{30 + 20 + 5 + 10}{4}$ = 16.25     [LOWEST]

Feb = $\frac{30 + 40 + 15 + 10}{4}$ = 23.75

Mar = $\frac{30 + 40 + 25 + 20}{4}$ = 28.75

Apr = $\frac{40 + 50 + 30 + 20}{4}$ = 35

May = $\frac{50 + 40 + 35 + 25}{4}$ = 37.5

Jun = $\frac{60 + 40 + 35 + 30}{4}$ = 41.25

Jul = $\frac{60 + 40 + 30 + 20}{4}$ = 37.5

Aug = $\frac{60 + 30 + 10 + 20}{4}$ = 30

=> Ans – (C)

23) Answer (D)

The sale of commodity A is constant from January to March and from June to August.

It kept increasing from March to June constantly.

Thus, Only in April, May and June, commodity A showed good increase.

=> Ans – (D)

24) Answer (D)

Total employees in both companies = 4800

=> Employees in company A = $\frac{5}{12} \times 4800 = 2000$

In company A, total males = $\frac{70}{100} \times 2000 = 1400$

Male employees who work in Ops = $\frac{60}{100} \times 1400 = 840$

=> Male employees who work in Admin = $\frac{1}{8} \times 560 = 70$

Total females in company A = $2000 – 1400 = 600$

Female employees who work in Admin = $\frac{24}{100} \times 600 = 144$

=> Female employees who work in Ops = $\frac{5}{8} \times 456 = 285$

=> Employees working in company B = $4800 – 2000 = 2800$

Similarly, employees working in company B :

Total males in company A = 70 + 840 + 490 = 1400

=> Required % = $\frac{490}{1400} \times 100 = 35 \%$

25) Answer (B)

Total employees in both companies = 4800

=> Employees in company A = $\frac{5}{12} \times 4800 = 2000$

In company A, total males = $\frac{70}{100} \times 2000 = 1400$

Male employees who work in Ops = $\frac{60}{100} \times 1400 = 840$

=> Male employees who work in Admin = $\frac{1}{8} \times 560 = 70$

Total females in company A = $2000 – 1400 = 600$

Female employees who work in Admin = $\frac{24}{100} \times 600 = 144$

=> Female employees who work in Ops = $\frac{5}{8} \times 456 = 285$

=> Employees working in company B = $4800 – 2000 = 2800$

Similarly, employees working in company B :

Total females in company B = 49 + 364 + 147 = 560

=> Required % = $\frac{49}{560} \times 100 = 8.75 \%$

26) Answer (D)

Total employees in both companies = 4800

=> Employees in company A = $\frac{5}{12} \times 4800 = 2000$

In company A, total males = $\frac{70}{100} \times 2000 = 1400$

Male employees who work in Ops = $\frac{60}{100} \times 1400 = 840$

=> Male employees who work in Admin = $\frac{1}{8} \times 560 = 70$

Total females in company A = $2000 – 1400 = 600$

Female employees who work in Admin = $\frac{24}{100} \times 600 = 144$

=> Female employees who work in Ops = $\frac{5}{8} \times 456 = 285$

=> Employees working in company B = $4800 – 2000 = 2800$

Similarly, employees working in company B :

Total number of female employees who work in Ops in Company A and B together = 285 + 364 = 649

27) Answer (A)

Total employees in both companies = 4800

=> Employees in company A = $\frac{5}{12} \times 4800 = 2000$

In company A, total males = $\frac{70}{100} \times 2000 = 1400$

Male employees who work in Ops = $\frac{60}{100} \times 1400 = 840$

=> Male employees who work in Admin = $\frac{1}{8} \times 560 = 70$

Total females in company A = $2000 – 1400 = 600$

Female employees who work in Admin = $\frac{24}{100} \times 600 = 144$

=> Female employees who work in Ops = $\frac{5}{8} \times 456 = 285$

=> Employees working in company B = $4800 – 2000 = 2800$

Similarly, employees working in company B :

Number of males working in ‘Admin’ in both the companies together = 70 + 196 = 266

=> Average = $\frac{266}{2} = 133$

Number of females working in ‘Other Departments’ in both the companies together = 171 + 147 = 318

=> Average = $\frac{318}{2} = 159$

$\therefore$ Difference = 159 – 133 = 26

28) Answer (B)

Total employees in both companies = 4800

=> Employees in company A = $\frac{5}{12} \times 4800 = 2000$

In company A, total males = $\frac{70}{100} \times 2000 = 1400$

Male employees who work in Ops = $\frac{60}{100} \times 1400 = 840$

=> Male employees who work in Admin = $\frac{1}{8} \times 560 = 70$

Total females in company A = $2000 – 1400 = 600$

Female employees who work in Admin = $\frac{24}{100} \times 600 = 144$

=> Female employees who work in Ops = $\frac{5}{8} \times 456 = 285$

=> Employees working in company B = $4800 – 2000 = 2800$

Similarly, employees working in company B :

In company B,

Total number of employees (both male and female) who work in ‘Admin’ = 196 + 49 = 245

Total number of employees (both male and female) who work in ‘Other department’ = 588 + 147 = 735

=> Required ratio = $\frac{245}{735} = 1 : 3$

29) Answer (B)

Number of cellular phones (both Nokia and Samsung) sold by store B

= $\frac{21}{100} \times 6400 = 1344$

Number of Nokia cellular phones sold by store A

= $\frac{24}{100} \times 3000 = 720$

=> Required % = $\frac{1344 – 720}{720} \times 100$

= $\frac{260}{3} = 86 \frac{2}{3} \%$

30) Answer (E)

% of cellular phones (both Nokia and Samsung) sold by store D = 33%

$\because 100 \% \equiv 360$°

=> $33 \% \equiv \frac{360}{100} \times 33$

= $118.8$°

31) Answer (B)

% of cellular phones (both nokia and samsung) sold by stores B,C and D together = (21 + 15 + 33)% = 69%

=> Number of cellular phones (both nokia and samsung) sold by stores B,C and D together

= $\frac{69}{100} \times 6400 = 4416$

% of nokia phones sold by stores B,C and D together = (18 + 20 + 30)% = 68%

=> Number of nokia phones sold by stores B,C and D together

= $\frac{68}{100} \times 3000 = 2040$

=> Total number of Samsung cellular phones sold by stores B, C and D = 4416 – 2040 = 2376

$\therefore$ Required average = $\frac{2376}{3} = 792$

32) Answer (B)

Number of cellular phones (both Nokia and Samsung) sold by store A

= $\frac{19}{100} \times 6400 = 1216$

% of Nokia cellular phones sold by stores B and E together = (18 + 8)% = 26%

=> Number of Nokia cellular phones sold by stores B and E together = $\frac{26}{100} \times 3000 = 780$

$\therefore$ Required difference = $1216 – 780 = 436$

33) Answer (A)

Total number of phones (both Nokia and Samsung) sold by store E = $\frac{12}{100} \times 6400 = 768$

Nokia phones sold by store E = $\frac{8}{100} \times 3000 = 240$

=> Samsung cellular phones sold by store E = $768 – 240 = 528$

Number of phones (both Nokia and Samsung) sold by store C = $\frac{15}{100} \times 6400 = 960$

=> Required % = $\frac{528}{960} \times 100 = 55\%$

34) Answer (E)

I : Let base of the triangle = $4x$ m

=> Height of triangle = $\frac{3}{4} \times 4x = 3x$ m

There is no other info, so I alone is insufficient.

Similarly, II alone is also insufficient.

Combining both statements, and using pythagoras theorem, we get :

=> $(3x)^2 + (4x)^2 = (5^2)$

=> $9x^2 + 16x^2 = 25$

=> $x^2 = \frac{25}{25} = 1$

=> $x = \sqrt{1} = 1$

=> Base = 4 m and height = 3 m

$\therefore$ Area of triangle = $\frac{1}{2} \times 3 \times 4 = 6 m^2$

Thus, both statements together are sufficient.

35) Answer (E)

I : Let present age of son = $x$ years

=> Present age of father = $5x$ years.

There is no other information, so statement I is not sufficient.

Similarly, II alone is not sufficient.

Combining both statements, we get :

=> $(5x – 5) = 15 (x – 5)$

=> $5x – 5 = 15x – 75$

=> $15x – 5x = 75 – 5$

=> $10x = 70$ => $x = \frac{70}{10} = 7$

$\therefore$ father’s age = $5 \times 7 = 35$ years.

Thus, both statements together are sufficient.

Free Banking Study Material (15,000 Solved Questions