Clocks & Calendars Questions for RRB Group-D PDF
Download Top-15 RRB Group-D Clocks & Calendars Questions PDF. RRB GROUP-D Clocks & Calendars questions based on asked questions in previous exam papers very important for the Railway Group-D exam.
Download Clocks & Calendars Questions for RRB Group-D PDF
Download RRB Group-D Previous Papers PDF
Take a RRB Group-D free mock test
Question 1: Find the mirror image of the clock when the time is 03:00
a) 08:57
b) 09:00
c) 09:03
d) 09:01
Question 2: If 15-06-1994 is wednesday, then what day is 19-07-1995 ?
a) Tuesday
b) Wednesday
c) Thursday
d) Friday
Question 3: What day is it after 178 days if it is a Monday tomorrow?
a) Tuesday
b) Saturday
c) Friday
d) Wednesday
Question 4: Which day is it on 1st January, 2000.
a) Monday
b) Wednesday
c) Saturday
d) Sunday
Take a free mock test for RRB Group-D
770 Mocks (cracku Pass) Just Rs.199
Question 5: At what time the hands of the clock show a mirror image of 4:10 ?
a) 7:10
b) 7:40
c) 7:50
d) 8:10
Question 6: At what time between 2 O’Clock and 3 O’Clock, will the minute hand and hour hand of the clock be exactly opposite to each other?
a) $02:46$
b) $02:47\dfrac{6}{11}$
c) $02:43\dfrac{7}{11}$
d) $02:47$
Question 7: Find the number of days in p weeks and p days.
a) 8p
b) $7p^2$
c) $8p^2$
d) 7p
Question 8: Find the total number of days present in the first century.
a) 36500
b) 36512
c) 36524
d) 36525
RRB Group D previous year papers
Question 9: Which of the following is not a leap year?
a) 1800
b) 1864
c) 1600
d) 1624
Question 10: Find the angle between the hands of the clock when the time is 10:30
a) $160^\circ$
b) $120^\circ$
c) $180^\circ$
d) $135^\circ$
Question 11: What day is it on 26th January, 1950?
a) Wednesday
b) Thursday
c) Friday
d) Saturday
RRB Group-D Important Questions (download PDF)
Question 12: Which of the following years has the same calendar as that of the year 1963?
a) 1971
b) 1972
c) 1973
d) 1974
Question 13: A clock shows 7 O’clock in the morning. By how much angle will the hours hand rotate when the clock shows 9 O’clock in the morning.
a) $40^\circ$
b) $60^\circ$
c) $45^\circ$
d) $90^\circ$
Question 14: Which of the following days cannot be the last day of the century?
a) Friday
b) Wednesday
c) Sunday
d) Saturday
Question 15: What will be the day of the week on 13th April, 2006?
a) Thursday
b) Saturday
c) Sunday
d) Tuesday
General Science Notes for RRB Exams (PDF)
Answers & Solutions:
1) Answer (B)
We need to subtract from 12:00 or 11:60 to get mirror image time
Mirror image of 03:00 = 12:00 – 03:00 = 09:00
2) Answer (B)
a non leap year has 365 days (52 weeks+1 day).
1995 is not a leap year, And 15-06-1994 is wednesday, So 15-06-1995 would be thursday.
And 19-07-1995 is 34th day after 15-06-1995 (thursday), ⇒ 34 = 7(4)+6 days, So 6th day after thursday is Wednesday.
So the answer is option B.
3) Answer (D)
If tomorrow is a Monday, then today is a Sunday.
178 = (7 * 25) + 3
178 days is equal to 25 weeks and 3 odd days.
3 days after a Sunday is a Wednesday.
Hence, it is a Wednesday after 178 days.
4) Answer (C)
The number of odd days in every 400 years = 0
=> 31st December 2000 is a Sunday.
=> 1st January 2001 is a Monday.
2000 is a leap year => It has 2 odd days.
So, the day on 1st January 2000 will be two days prior to a Monday.
Hence, 1st January 2000 is a Saturday.
5) Answer (C)
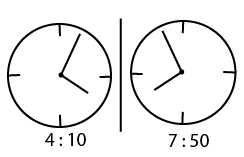
It should be 7:50
So the answer is option C.
6) Answer (C)
Angle between two hands $= \dfrac{11}{2}M – 30H$ where H is hours and M is Minutes
Here, H = 2 and Angle = $180^\circ$
$180^\circ = \dfrac{11}{2}M – 30\times2$
⇒ $\dfrac{11}{2}M = 240$
⇒ $M = \dfrac{480}{11} = 43\dfrac{7}{11}$
Hence, the required time = $02:43\dfrac{7}{11}$
7) Answer (A)
Each week has 7 days.
p weeks => 7p days.
So, the total number of days in p weeks and p days = 7p + p = 8p days
8) Answer (C)
There are 76 ordinary years and 24 leap years in the first century.
=> Number of days = (76 * 365) + (24 * 366)
= (100 * 365) + 24
= 36524
9) Answer (A)
We know that all the years that are a multiple of 4 but are not centuries are leap years.
Hence, 1864 and 1624 are leap years.
Also, all the years that are multiple of 400 are leap years.
Hence, 2000 is a leap year.
=> 1800 is not a leap year.
10) Answer (D)
Required angle $= 30H – \dfrac{11}{2}M$ where H is hours and M is Minutes
Here, H = 10 and M = 30
Hence, Required angle $= 30\times10 – \dfrac{11}{2}\times30$
$= 300 – 165 = 135^\circ$
11) Answer (B)
1949 = 1600 + 349
We know that after every 400 years, the number of odd days is 0.
Hence, after 1600 years, the number of odd days is 0.
350 = 300 + 50.
We know that after every 300 years, there is exactly 1 odd day.
In next 49 years, there are 12 leap years and 37 ordinary years.
=> Number of odd days until 31st December 1949 = (12 * 2) + (37 * 1) + 1 = 24 + 37 + 1 = 62
Total number of odd days until 26th January, 1950 = 26 + 62 = 88
88 = (7 * 12) + 4
=> 4 odd days
=> It is a Thursday.
12) Answer (D)
On counting the number of odd days from 1963 to the year that has the same calendar as that of 1963, we must get 0 odd number of days.
Let’s calculate the number of number of odd days up to 1970.
1963 has 1 odd day.
1964 has 2 odd days.
1965 has 1 odd day.
1966 has 1 odd day.
1967 has 1 odd day.
1968 has 2 odd days.
1969 has 1 odd day.
1970 has 1 odd day.
Sum of the odd days until 1970 is 10.
10 = (1 * 7) + 3 => Number of odd days is not 0 => 1971 does not have the same calendar as 1963.
1971 has 1 odd day.
Sum of the odd days until 1971 is 11.
11 = (1 * 7) + 4 => Number of odd days is not 0 => 1972 does not have the same calendar as 1963.
1972 has 2 odd days.
Sum of the odd days until 1972 is 13.
13 = (1 * 7) + 6 => Number of odd days is not 0 => 1973 does not have the same calendar as 1963.
1973 has 1 odd day.
Sum of the odd days until 1973 is 14.
14 = (2 * 7) + 0 => Number of odd days is 0 => 1974 has the same calendar as 1963.
13) Answer (B)
In 12 hours, the hand turns $360^\circ$.
Here, the difference between time = 2 hours
Then, Required angle $= \dfrac{360}{12}\times2 = 60^\circ$
14) Answer (D)
Let’s calculate the number of odd days is 100 years.
In 100 years, there are 76 ordinary years and 24 leap years.
So, in 100 years, there are (76*1) + (24*2) odd days, which is equal to 124 odd days.
124 = (7 * 17) + 5
So, 124 days is equal to 17 weeks and 5 odd days. Hence, 100 years have 5 odd days => Friday
In 200 years, there are 2*5 odd days, which is equal to 10 days.
10 = (7 * 1) + 3
So, 10 days is equal to 1 week and 3 odd days. Hence, 200 years have 3 odd days.
In 300 years, there are 3*5 odd days, which is equal to 15 days.
15 = (7 * 2) + 1
So, 15 days is equal to 2 weeks and 1 odd day. Hence, 300 years have 1 odd day.
In 400 years, there are (4 * 5 + 1) odd days. 1 is added because every 4th century is a leap year. So, there are 21 odd days in every 400 years.
21 = (7 * 3) + 0
Hence, there are 0 odd days in every 400 years => Sunday
So, only Sunday, Monday, Wednesday and Friday can be the last day of the century.
Among the given options, only Saturday cannot be the last day of the century.
15) Answer (A)
We know that the number of odd days in every 400 years is 0.
Hence, the number of odd days in 2000 years is 0.
In the remaining 5 years, there are 4 ordinary years and 1 leap year.
=> There are (4 * 1) + (1 * 2) = 6 odd days until December 31st, 2005.
The number of days in 2006 until 13th April is 31 + 28 + 31 + 13 = 103.
6 + 103 = 109
109 = (7 * 15) + 4.
4 odd days => It is a Thursday on 13th April 2006.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Clocks & Calendars Questions PDF for RRB Group-D Exam will be highly useful for your preparation.







