CAT Venn Diagrams Questions PDF
Venn Diagrams is one of the important topics in the CAT Quant/LRDI section. These questions can be a bit challenging, so ensure that you are aware of the Important ways to represent and solve Venn Diagrams in Quant/LRDI. You can check out these CAT Venn Diagrams questions from the CAT Previous year papers. This post will look into some important Venn Diagrams for CAT. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download these Important Venn Diagrams Questions for CAT (with detailed answers) PDF below, which is completely Free.
Download Venn Diagrams Questions for CAT
Enroll for CAT 2022 Crash Course
Question 1: Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
a) 32
b) 24
c) 30
d) None of these
1) Answer (C)
Solution:
Let the number of total days=N
They played tennis for=N-14 days
They did yoga for =N-24 days
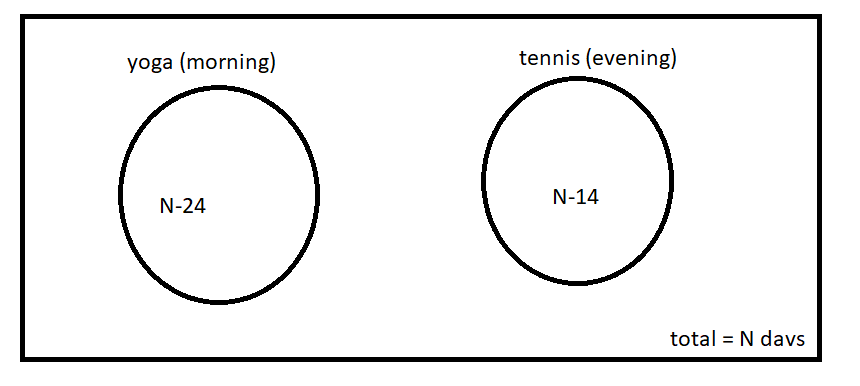
And the question says that total days when they did yoga or played tennis are 22
which means
N-14 + N-24 = 22
2N – 38 = 22
2N = 60
N = 30
Hence total days they stayed together were 30
Instructions
There were a hundred schools in a town. Of these, the number of schools having a play – ground was 30, and these schools had neither a library nor a laboratory. The number of schools having a laboratory alone was twice the number of those having a library only. The number of schools having a laboratory as well as a library was one-fourth the number of those having a laboratory alone. The number of schools having either a laboratory or a library or both was 35.
Question 2: How many schools had none of the three viz., laboratory, library or play – ground?
a) 20
b) 5
c) 30
d) 35
2) Answer (D)
Solution:

The diagram for this question has been shown:
Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35
Here a = b = y = 0
7x/2 = 35
x = 10
Total number of schools having at least one of PG, LIB or LAB = 30+2x+x+x/2 = 30+3x+x/2 = 30+30+5 = 65
Number of schools having neither of the three = 100-65 = 35
Question 3: What was the ratio of schools having laboratory those having library?
a) 1 : 2
b) 5 : 3
c) 2 : 1
d) 2 : 3
3) Answer (B)
Solution:

The diagram for this question has been shown:
Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35
It has been given that the schools having playground don’t have a Library or Laboratory.
Hence a = b = y = 0
7x/2 = 35
x = 10
Required ratio = 25:15 = 5:3
InstructionsA survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and
DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.
Question 4: What is the maximum percentage of people who can watch all the three channels?
a) 12.5%
b) 8.5%
c) 15%
d) Data insufficient
4) Answer (B)
Solution:
Let a be the number who watch only one channel, b be the number who watch only 2 channels and c be the number who watch all channels.
a+b+c = 100
a+2b+3c = 80+22+15 =117
Subtracting both equations,
b+2c = 117-100 = 17
Maximum c occurs when b = 0
2c = 17
c = 8.5
Question 5: If 5% of people watched DD and CNN, 10% watched DD and BBC, then what percentage of people watched BBC and CNN only?
a) 2%
b) 5%
c) 8.5%
d) Cannot be determined
5) Answer (A)
Solution:
Applying AUBUC formula
Let x be the number who watch BBC and CNN and y be the number who watch all three channels.
100 = 80+22+15-(10+5+x)+y
x-y = 2
Hence only 2% people watch BBC and CNN only.
Checkout: CAT Free Practice Questions and Videos
Question 6: Referring to the previous question, what percentage of people watched all the three channels?
a) 3.5%
b) 0%
c) 8.5%
d) Cannot be determined
6) Answer (D)
Solution:
Applying AUBUC formula
Let x be the number who watch BBC and CNN and y be the number who watch all three channels.
100 = 80+22+15-(10+5+x)+y
x-y = 2
We cannot find the exact value of y.
Hence, the answer is “cannot be determined”.
Question 7: Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
7) Answer: 52
Solution:
Let us draw a Venn diagram using the information present in the question.
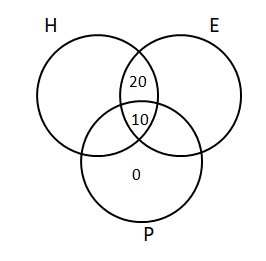
It is given that the number of students studying H equals that studying E.
Let ‘x’ be the total number of students who studied H, and H and P but mot E.We can also say that the same will be the number of students who studied E, and E and P but not H.Therefore,
x + 20 + 10 + x = 74
x = 22
Hence, the number of students studying H = 22 + 10+ 20 = 52
Question 8: If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
a) 23
b) 26
c) 96
d) 93
8) Answer (D)
Solution:
It has been given that among 200 students, 105 like pizza and 134 like burger.
The question asks us to find out the number of students who can be liking only burgers among the given values.
The least number of students who like only burger will be obtained when everyone who likes pizza likes burger too.
In this case, 105 students will like pizza and burger and 134-105 = 29 students will like only burger. Therefore, the number of students who like only burger cannot be less than 29.
The maximum number of students who like only burger will be obtained when we try to separate the 2 sets as much as possible.
There are 200 students in total. 105 of them like pizza. Therefore, the remaining 95 students can like only burger and 134-95 = 39 students can like both pizza and burger. As we can see, the number of students who like burger cannot exceed 95.
The number of students who like only burger should lie between 29 and 95 (both the values are included).
93 is the only value among the given options that satisfies this condition and hence, option D is the right answer.
Question 9: For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6,}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
9) Answer: 7
Solution:
P = {1,2,3,4} and Q = {2,3,5,6,}
PΔQ = {1, 4, 5, 6}
R = {1,3,7,8,9} and S = {2,4,9,10}
RΔS = {1, 2, 3, 4, 7, 8, 10}
(PΔQ)Δ(RΔS) = {2, 3, 5, 6, 7, 8, 10}
Thus, there are 7 elements in (PΔQ)Δ(RΔS) .
hence, 7 is the correct answer.
Question 10: If A = {$6^{2n} -35n – 1$}, where $n$ = 1,2,3,… and B = {35($n$-1)}, where $n$ = 1,2,3,… then which of the following is true?
a) Every member of A is in B and at least one member of B is not in A
b) Neither every member of A is in B nor every member of B is in A
c) Every member of B is in A.
d) At least one member of A is not in B
10) Answer (A)
Solution:
If we carefully observe set A, then we find that $6^{2n} -35n – 1$ is divisible by 35. So, set A contains multiples of 35. However, not all the multiples of 35 are there in set A, for different values of $n$.
For $n = 1$, the value is 0, for $n = 2$, the value is 1225 which is the 35th multiple of 3.
If we observe set B, it consists of all the multiples of 35 including 0.
So, we can say that every member of set A will be in B while every member of set B will not necessarily be in set A.
Hence, option A is the correct answer.
Question 11: A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
a) 38
b) 32
c) 45
d) 43
11) Answer (D)
Solution:
Assume the number of members who can play exactly 1 game = I
The number of members who can play exactly 1 game = II
The number of members who can play exactly 1 game = III
I+2II+3III=144+123+132=399….(1)
I+II+III=256……(2)
=> II+2III=143…..(3)
Also, II+3III=58+25+63=146 ……(4)
=> III = 3 (From 3 and 4)
=> II =137
=> I = 116
The members who play only tennis = 123-58-25+3 = 43
Question 12: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
a) 22
b) 21
c) 20
d) 19
12) Answer (C)
Solution:
Now 23 students choose maths as one of their subject.
This means (MPC)+ (MC) + (PC)=23 where MPC denotes students who choose all the three subjects maths, physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP =7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM=5 and MC=0. In the second equation this PC=2
Hence minimum number of students choosing chemistry will be (18+2)=20 Since 18 students chose all the three subjects.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
