CAT Inequalities Questions PDF [Most Important]

Inequalities is an important topic in the CAT Quant (Algebra) section. If you find these questions a bit tough, make sure you solve more CAT Inequalities questions. Learn all the important formulas and tricks on how to answer questions on Inequalities. You can check out these CAT Inequalities questions from the CAT Previous year papers. Practice a good number of sums in the CAT Inequalities so that you can answer these questions with ease in the exam. In this post, we will look into some important Inequalities Questions for CAT quants. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download this Important CAT Inequalities Questions and answers PDF along with the video solutions below, which is completely Free.

Download Inequalites Questions for CAT

Enroll for CAT 2022 Crash Course

Question 1: If n is a positive integer such that $(\sqrt[7]{10})(\sqrt[7]{10})^{2}…(\sqrt[7]{10})^{n}>999$, then the smallest value of n is

1) Answer: 6

View Video Solution

Solution:

$(\sqrt[7]{10})(\sqrt[7]{10})^{2}…(\sqrt[7]{10})^{n}>999$

$(\sqrt[7]{10})^{1+2+…+n}>999$

$10^{\frac{1+2+…+n}{7}}>999$

For minimum value of n,

$\frac{1+2+…+n}{7}=3$

1 + 2 + … + n = 21

We can see that if n = 6, 1 + 2 + 3 + … + 6 = 21.

Question 2: The number of distinct pairs of integers (m,n), satisfying $\mid1+mn\mid<\mid m+n\mid<5$ is:

2) Answer: 12

View Video Solution

Solution:

Let us break this up into 2 inequations [ Let us assume x as m and y as n ]

| 1 + mn | < | m + n |

| m + n | < 5

Looking at these expressions, we can clearly tell that the graphs will be symmetrical about the origin.

Let us try out with the first quadrant and extend the results to the other quadrants.

We will also consider the +X and +Y axes along with the quadrant.

So, the first inequality becomes,

1 + mn < m + n

1 + mn – m – n < 0

1 – m + mn – n < 0

(1-m) + n(m-1) < 0

(1-m)(1-n) < 0

(m – 1)(n – 1) < 0

Let us try to plot the graph.

If we consider only mn < 0, then we get

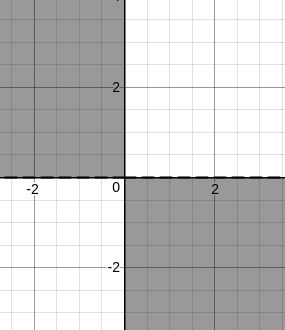
But, we have (m – 1)(n – 1) < 0, so we need to shift the graphs by one unit towards positive x and positive y.

So, we have,

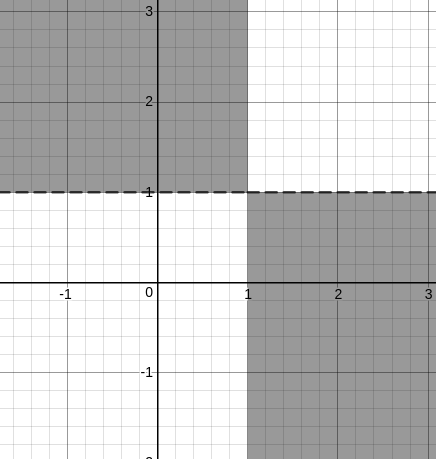
But, we are only considering the first quadrant and the +X and +Y axes. Hence, if we extend, we get the following region.

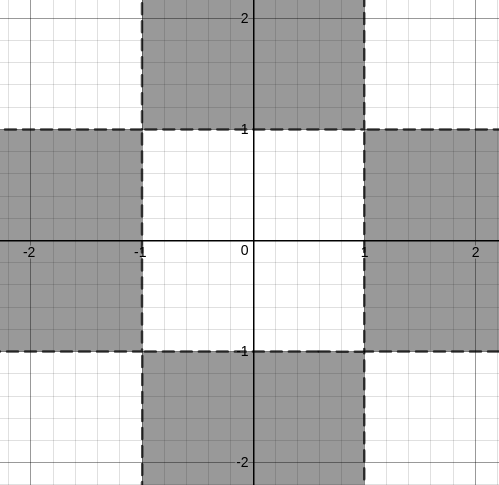
So, if we look for only integer values, we get

(0,2), (0,3),…….

(0,-2), (0, -3),……

(2,0), (3,0), ……

(-2,0), (-3,0), …….

Now, let us consider the other inequation as well, in which |x + y| < 5

Since one of the values is always zero, the modulus of the other value is less than or equal to 4.

Hence, we get

(0,2), (0,3), (0,4)

(0,-2), (0, -3), (0, -4)

(2,0), (3,0), (4,0)

(-2,0), (-3,0), (-4,0)

Hence, a total of 12 values.

Question 3: For a real number x the condition $\mid3x-20\mid+\mid3x-40\mid=20$ necessarily holds if

a) $10<x<15$

b) $9<x<14$

c) $7<x<12$

d) $6<x<11$

3) Answer (C)

View Video Solution

Solution:

Case 1 : $x\ge\frac{40}{3}$
we get 3x-20 +3x-40 =20
6x=80
x=$\frac{80}{6}$=$\frac{40}{3}$=13.33
Case 2 :$\frac{20}{3}\le\ x<\frac{40}{3}\ $
we get 3x-20+40-3x =20
we get 20=20
So we get x$\in\ \left[\frac{20}{3},\frac{40}{3}\right]$
Case 3 $x<\frac{20}{3}$
we get 20-3x+40-3x =20
40=6x
x=$\frac{20}{3}$
but this is not possible
so we get from case 1,2 and 3
$\frac{20}{3}\le\ x\le\frac{40}{3}$
Now looking at options
we can say only option C satisfies for all x .
Hence 7<x<12.

Question 4: $f(x) = \frac{x^2 + 2x – 15}{x^2 – 7x – 18}$ is negative if and only if

a) -5 < x < -2 or 3 < x < 9

b) x < -5 or -2 < x < 3

c) -2 < x < 3 or x > 9

d) x < -5 or 3 < x < 9

4) Answer (A)

View Video Solution

Solution:

$f(x) = \frac{x^2 + 2x – 15}{x^2 – 7x – 18}$<0

$\frac{\left(x+5\right)\left(x-3\right)}{\left(x-9\right)\left(x+2\right)}<0$

We have four inflection points -5, -2, 3, and 9.

For x<-5, all four terms (x+5), (x-3), (x-9), (x+2) will be negative. Hence, the overall expression will be positive. Similarly, when x>9, all four terms will be positive.

When x belongs to (-2,3), two terms are negative and two are positive. Hence, the overall expression is positive again.

We are left with the range (-5,-2) and (3,9) where the expression will be negative.

Question 5: The number of integers n that satisfy the inequalities $\mid n – 60 \mid < \mid n – 100 \mid < \mid n – 20 \mid$ is

a) 21

b) 19

c) 18

d) 20

5) Answer (B)

View Video Solution

Solution:

We have $\mid n – 60 \mid < \mid n – 100 \mid < \mid n – 20 \mid$.

Now, the difference inside the modulus signified the distance of n from 60, 100, and 20 on the number line. This means that when the absolute difference from a number is larger, n would be further away from that number.

Example: The absolute difference of n and 60 is less than that of the absolute difference between n and 20. Hence, n cannot be $\le\ 40$, as then it would be closer to 20 than 60, and closer on the number line would indicate lesser value of absolute difference. Thus we have the condition that n>40.

The absolute difference of n and 100 is less than that of the absolute difference between n and 20. Hence, n cannot be $\le\ 60$, as then it would be closer to 20 than 100. Thus we have the condition that n>60.

The absolute difference of n and 60 is less than that of the absolute difference between n and 100. Hence, n cannot be $\ge80$, as then it would be closer to 100 than 60. Thus we have the condition that n<80.

The number which satisfies the conditions are 61, 62, 63, 64……79. Thus, a total of 19 numbers.

Alternatively

as per the given condition : $\mid n – 60 \mid < \mid n – 100 \mid < \mid n – 20 \mid$.

Dividing the range of n into 4 segments. (n < 20, 20<n<60, 60<n<100, n > 100 )

1) For n < 20.

|n-20| = 20-n, |n-60| = 60- n, |n-100| = 100-n

considering the inequality part :$\left|n-100\right|<\ \left|n\ -20\right|$

100 -n < 20 -n,

No value of n satisfies this condition.

2) For 20 < n < 60.

|n-20| = n-20, |n-60| = 60- n, |n-100| = 100-n.

60- n < 100 – n and 100 – n < n – 20

For 100 -n < n – 20.

120 < 2n and n > 60. But for the considered range n is less than 60.

3) For 60 < n < 100

|n-20| = n-20, |n-60| = n-60, |n-100| = 100-n

n-60 < 100-n and 100-n < n-20.

For the first part 2n < 160 and for the second part 120 < 2n.

n takes values from 61 …………….79.

A total of 19 values

4) For n > 100

|n-20| = n-20, |n-60| = n-60, |n-100| = n-100

n-60 < n – 100.

No value of n in the given range satisfies the given inequality.

Hence a total of 19 values satisfy the inequality.

Checkout: CAT Free Practice Questions and Videos

Question 6: if x and y are positive real numbers satisfying $x+y=102$, then the minimum possible valus of $2601(1+\frac{1}{x})(1+\frac{1}{y})$ is

6) Answer: 2704

View Video Solution

Solution:

Now we have $2601\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)=2601\left(\frac{xy+y+x+1}{xy}\right)$

Now we know that x+y=102. Substituting it in the above equation

$2601\left(\frac{xy+y+x+1}{xy}\right)=2601\left(\frac{103}{xy}+1\right)$

Maximum value of xy  can be found out by AM>= GM relationship

$\ \frac{\ x+y}{2}\ge\ \sqrt{xy}\ or\ \ \sqrt{\ xy}\le\ 51\ or\ xy\le\ 2601$

Hence the maximum value of “xy” is 2601. Substituting in the above equation we get

$2601\left(\ \frac{\ 103+2601}{2601}\right)=2704$

Question 7: For real x, the maximum possible value of $\frac{x}{\sqrt{1+x^{4}}}$ is

a) $\frac{1}{2}$

b) $1$

c) $\frac{1}{\sqrt{3}}$

d) $\frac{1}{\sqrt{2}}$

7) Answer (D)

View Video Solution

Solution:

Now $\frac{x}{\sqrt{\ 1+x^4}}=\ \frac{\ 1}{\sqrt{\ \ \frac{\ 1+x^4}{x^2}}}=\frac{1}{\sqrt{\ \frac{1}{x^2}+x^2}}$

Applying A.M>= G.M.

$\frac{\left(\frac{1}{x^2}+x^2\right)}{2}\ge\ 1\ or\ \ \frac{1}{x^2}+x^2\ge\ 2$ Substituting we get the maximum possible value of the equation as $\frac{1}{\sqrt{\ 2}}$

Question 8: The number of pairs of integers $(x,y)$ satisfying $x\geq y\geq-20$ and $2x+5y=99$

8) Answer: 17

View Video Solution

Solution:

We have 2x + 5y = 99 or $x=\frac{\left(99-5y\right)}{2}$

Now $x\ge\ y\ \ge\ -20$ ; So $\frac{\left(99-5y\right)}{2}\ge\ y\ ;\ 99\ge7y\ or\ y\le\ \approx\ 14$

So $-20\le y\le14$. Now for this range of “y”, we have to find all the integral values of “x”. As the coefficient of “x” is 2,

then (99 – 5y) must be even, which will happen when “y” is odd. However, there are only 17 odd values of “y” be -20 and 14.

Hence the number of possible values is 17.

Question 9: Among 100 students, $x_1$ have birthdays in January, $X_2$ have birthdays in February, and so on. If $x_0=max(x_1,x_2,….,x_{12})$, then the smallest possible value of $x_0$ is

a) 8

b) 9

c) 10

d) 12

9) Answer (B)

View Video Solution

Solution:

$x_0=max(x_1,x_2,….,x_{12})$

$x_0$ will be minimum if x1,x2…x12 are close to each other

100/12=8.33

.’. max$(x_1,x_2,….,x_{12})$ will be minimum if $(x_1,x_2,….,x_{12})$=(9,9,9,9,8,8,8,8,8,8,8,8,)

.’. Option B is correct.

Question 10: If x is a real number, then $\sqrt{\log_{e}{\frac{4x – x^2}{3}}}$ is a real number if and only if

a) $1 \leq x \leq 3$

b) $1 \leq x \leq 2$

c) $-1 \leq x \leq 3$

d) $-3 \leq x \leq 3$

10) Answer (A)

View Video Solution

Solution:

$\sqrt{\log_{e}{\frac{4x – x^2}{3}}}$ will be real if $\log_e\ \frac{\ 4x-x^2}{3}\ \ge\ 0$

$\frac{\ 4x-x^2}{3}\ >=\ 1$

$\ 4x-x^2-3\ >=\ 0$

$\ x^2-4x+3\ =<\ 0$

1=< x=< 3

Question 11: The smallest integer $n$ such that $n^3-11n^2+32n-28>0$ is

11) Answer: 8

View Video Solution

Solution:

We can see that at n = 2, $n^3-11n^2+32n-28=0$ i.e. (n-2) is a factor of $n^3-11n^2+32n-28$

$\dfrac{n^3-11n^2+32n-28}{n-2}=n^2-9n+14$

We can further factorize n^2-9n+14 as (n-2)(n-7).

$n^3-11n^2+32n-28=(n-2)^2(n-7)$

$\Rightarrow$ $n^3-11n^2+32n-28>0$

$\Rightarrow$ $(n-2)^2(n-7)>0$

Therefore, we can say that n-7>0

Hence, n$_{min}$ = 8

Question 12: The minimum possible value of the sum of the squares of the roots of the equation $x^2+(a+3)x-(a+5)=0 $ is

a) 1

b) 2

c) 3

d) 4

12) Answer (C)

View Video Solution

Solution:

Let the roots of the equation $x^2+(a+3)x-(a+5)=0 $ be equal to $p,q$

Hence, $p+q = -(a+3)$ and $p \times q = -(a+5)$

Therefore, $p^2+q^2 = a^2+6a+9+2a+10 = a^2+8a+19 = (a+4)^2+3$

As $(a+4)^2$ is always non negative, the least value of the sum of squares is 3

Question 13: For how many integers n, will the inequality $(n – 5) (n – 10) – 3(n – 2)\leq0$ be satisfied?

13) Answer: 11

View Video Solution

Solution:

$(n – 5) (n – 10) – 3(n – 2)\leq0$
=> $ n^2 – 15n + 50 – 3n + 6 \leq 0$
=> $n^2 – 18n + 56 \leq 0$
=> $(n – 4)(n – 14) \leq 0$
=> Thus, n can take values from 4 to 14. Hence, the required number of values are 14 – 4 + 1 = 11.

Question 14: If a and b are integers of opposite signs such that $(a + 3)^{2} : b^{2} = 9 : 1$ and $(a -1)^{2}:(b – 1)^{2} = 4:1$, then the ratio $a^{2} : b^{2}$ is

a) 9:4

b) 81:4

c) 1:4

d) 25:4

14) Answer (D)

View Video Solution

Solution:

Since the square root can be positive or negative we will get two cases for each of the equation.

For the first one,

a + 3 = 3b .. i

a + 3 = -3b … ii

For the second one,

a – 1 = 2(b -1) … iii

a – 1 = 2 (1 – b) … iv

we have to solve i and iii, i and iv, ii and iii, ii and iv.

Solving i and iii,

a + 3 = 3b and a = 2b  – 1, solving, we get a = 3 and b = 2, which is not what we want.

Solving i and iv

a + 3 = 3b and a = 3 – 2b, solving, we get b = 1.2, which is not possible.

Solving ii and iii

a + 3 = -3b and a = 2b – 1, solving, we get b = 0.4, which is not possible.

Solving ii and iv,

a + 3 = -3b and a = 3 – 2b, solving, we get a = 15 and b = -6 which is what we want.

Thus, $\frac{a^2}{b^2} = \frac{25}{4}$

Question 15: If | r – 6 | = 11 and | 2q – 12 | = 8, what is the minimum possible value of q / r?

a) -2/5

b) 2/17

c) 10/17

d) None of these

15) Answer (D)

View Video Solution

Solution:

| r-6 | = 11 => r = -5 or 17

| 2q – 12 | = 8 => q = 10 or 2

So, the minimum possible value of q/r = 10/(-5) = -2

Question 16: The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:

a) 59

b) 57

c) 55

d) 58

16) Answer (A)

View Video Solution

Solution:

y = $\frac{4x-1}{17}$

The integral values of x for which y is an integer are 13, 30, 47,……

The values are in the form 17n + 13, where $ n \geq 0$

17n + 13 < 1000

=> 17n < 987

=> n < 58.05

=> n can take values from 0 to 58 => Number of values = 59

Question 17: Which of the following values of x do not satisfy the inequality $(x^2 – 3x + 2 > 0)$ at all?

a) $1\leq x \leq 2$

b) $-1\geq x \geq -2$

c) $0 \leq x \leq 2$

d) $0\geq x \geq -2$

17) Answer (A)

View Video Solution

Solution:

After solving given equation, we will have inequality resolved to:

(x-1)(x-2)>0

Or we can say range of x will be as follows:

x<1;  x>2

Hence, option A has a set of values which don’t lie in the possible range of x.

So the answer will be A.

Question 18: The number of integers n satisfying -n+2 ≥ 0 and 2n ≥ 4 is

a) 0

b) 1

c) 2

d) 3

18) Answer (B)

View Video Solution

Solution:

-n+2 >= 0
or n<=2
and 2n>=4
or n>=2
So we can take only one value of n i.e. 2

Question 19: If pqr = 1, the value of the expression $1/(1+p+q^{-1}) + 1/(1+q+r^{-1}) + 1/(1+r+p^{-1})$

a) p+q+r

b) 1/(p+q+r)

c) 1

d) $p^{-1} + q^{-1} + r^{-1}$

19) Answer (C)

View Video Solution

Solution:

Let p = q = r = 1

So, the value of the expression becomes 1/3 + 1/3 + 1/3 = 1

If we substitute these values, options a), b) and d) do not satisfy.

Option c) is the answer.

Question 20: What values of x satisfy $x^{2/3} + x^{1/3} – 2 <= 0$?

a) $-8 \leq x \leq 1$

b) $-1 \leq x \leq 8$

c) $1 \leq x \leq 8$

d) $1 \leq x \leq 18$

e) $-8 \leq x \leq 8$

20) Answer (A)

View Video Solution

Solution:

Try to solve this type of questions using the options.

Subsitute 0 first => We ger -2 <=0, which is correct. Hence, 0 must be in the solution set.

Substitute 8 => 4 + 2 – 2 <=0 => 6 <= 0, which is false. Hence, 8 must not be in the solution set.

=> Option 1 is the answer.