CAT Geometry Circle Questions [Download PDF]

Geometry Circle is one of the most important topics in the CAT Quants section. If you’re weak in Geometry Circle questions for CAT, make sure you learn all the basic concepts of solving the questions and also all the important formulas. Here, you can learn all the important questions on the concept of CAT Geometry Circle. You can check out these CAT Geometry Circle questions from the CAT Previous year’s papers. This post will look at important Geometry Circle questions in the CAT quant section. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download this CAT TSD Questions PDF along with the detailed solutions (and video solutions) below, which is completely Free.

Download Geometry Questions for CAT

Enroll for CAT 2023 Crash Course

Question 1: Consider a square ABCD with midpoints E, F, G, H of AB, BC, CD and DA respectively. Let L denote the line passing through F and H. Consider points P and Q, on L and inside ABCD such that the angles APD and BQC both equal 120°. What is the ratio of the area of ABQCDP to the remaining area inside ABCD?

a) $\frac{4 \sqrt 2}{3}$

b) $2 + \sqrt{3}$

c) $\frac{10-3\sqrt{3}}{9}$

d) $1+\frac{1}{\sqrt3}$

e)  $2\sqrt{3}-1$

1) Answer (E)

View Video Solution

Solution:

Consider side of square as 10 units. So HD=5 and HP=$\frac{5}{\sqrt3}$ . So now area of triangle HPD=$\frac{12.5}{\sqrt3}$. Also Area APD=Area BQC=2*AreaHPD=$\frac{25}{\sqrt3}$. So numerator of required answer is $100-\frac{50}{\sqrt3}$ and denominator as $\frac{50}{\sqrt3}$. Solving we get answer as $2\sqrt{3}-1$.

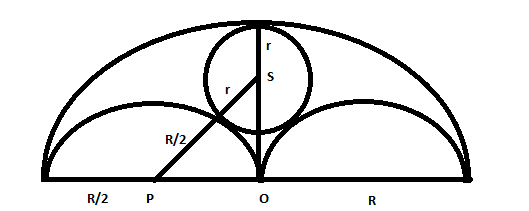
Question 2: Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centers at P and R respectively, and S is the center of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

a) 20

b) 28

c) 36

d) 40

2) Answer (B)

View Video Solution

Solution:

Let R be radius of big circle and r be radius of circle with centre S. Radius of 2 semicircles is R/2.

From Right angled triangle OPS, using pythagoras theorem we get

$(r+0.5R)^2 = (0.5R)^2 + (R-r)^2$ . We get R=3r .

Now the area of big semicircle that cannot be grazed is Area of big S.C – area of 2 semicircle – area of small circle = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*r^2$ = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*(R/3)^2$= $\pi*R^2$/2 – $\pi*(R)^2$/4-$\pi*(R)^2$/9 = 5*$\pi*R^2$/36.  this is about 28 % of the area $\pi*R^2$/2 . Hence option B.

Question 3: In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?

a) 10 cm

b) 40 cm

c) 50 cm

d) None of the above.

3) Answer (C)

View Video Solution

Solution:

As seen in the fig. we have a right angled triangle with sides  r ,r-10 , r-20.

Using pythagoras we have $r^2 = (r-10)^2 + (r-20)^2$.

Solving the equation, we get r = 10 or 50.

But 10 is not possible , so r = 50.

Hence radius is 50.

Question 4: Let $C$ be a circle with centre $P_0$ and $AB$ be a diameter of $C$. Suppose $P_1$ is the mid point of the line segment $P_0B$,$P_2$ is the mid point of the line segment $P_1B$ and so on. Let $C_1,C_2,C_3,…$ be circles with diameters $P_0P_1, P_1P_2, P_2P_3…$ respectively. Suppose the circles $C_1, C_2, C_3,…$ are all shaded. The ratio of the area of the unshaded portion of $C$ to that of the original circle is

a) 8 : 9

b) 9 : 10

c) 10 : 11

d) 11 : 12

4) Answer (D)

View Video Solution

Solution:

Radius of the circles $C_1, C_2, C_3,…$ would be in GP with (R/4),(R/8),(R/16) and so on. Radii of circles are in the ratio 1:4.

Ratio of unshaded region to the ratio of original circle = 1-$\frac{Ratio\ of\ shaded\ region}{Ratio\ of\ original\ circle}$

= 1-$\frac{\pi r^2/16 + \pi r^2/64+…..}{\pi r^2}$ = 1-$\frac{1/16}{(1-1/4)}$ = 1- 1/12 = $\frac{11}{12}$ = 11:12

Question 5: Rectangular tiles each of size 70 cm by 30 cm must be laid horizontally on a rectangular floor of size 110 cm by 130 cm, such that the tiles do not overlap. A tile can be placed in any orientation so long as its edges are parallel to the edges of the floor. No tile should overshoot any edge of the floor. The maximum number of tiles that can be accommodated on the floor is

a) 4

b) 5

c) 6

d) 7

5) Answer (C)

View Video Solution

Solution:

As seen from the fig. If following configuration is used max 6 number of tiles that can be accommodated on the floor.

Checkout: CAT Free Practice Questions and Videos

Question 6: A square, whose side is 2 m, has its corners cut away so as to form an octagon with all sides equal. Then the length of each side of the octagon, in metres, is

a) $ \frac{\sqrt 2}{\sqrt 2 +1} $

b) $\frac{2}{\sqrt 2 + 1} $

c) $\frac{2}{\sqrt 2 – 1}$

d) $\frac{\sqrt 2}{\sqrt 2-1} $

6) Answer (B)

View Video Solution

Solution:

Let the length of each side of the octagon be x.

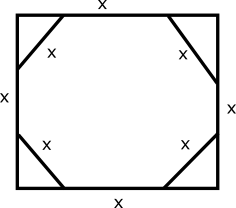
So, length of the square will be x+2*(x/√2) = 2

=> x(1+√2) = 2 => x = 2/(1+√2)

Question 7: A rectangular pool of 20 m wide and 60 m long is surrounded by a walkway of uniform width. If the total area of the walkway is 516 $m^2$ , how wide, in metres, is the walkway?

a) 4 m

b) 2 m

c) 3 m

d) 3.5 m

7) Answer (C)

View Video Solution

Solution:

If the width of the walkway is x, then its area = (60+2x)(20+2x) – 1200 = 516
Solving this, we get x = 3m

Question 8: If a,b,c are the sides of a triangle, and $a^2 + b^2 +c^2 = bc + ca + ab$, then the triangle is:

a) equilateral

b) isosceles

c) right angled

d) obtuse angled

8) Answer (A)

View Video Solution

Solution:

$(a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) => 3(a^2 + b^2 + c^2)$

This is possible only if a = b = c.

So, the triangle is an equilateral triangle.

Question 9: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centers of the circles. The distance PQ is

The length of AB is 15 m and AC is 20 m

a) 7 m

b) 4.5 m

c) 10.5 m

d) 6 m

9) Answer (A)

View Video Solution

Solution:

By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16

We know that AREA = (semi perimeter ) * inradius

For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.

Similarly for triangle ADC we get inradius R = 4 .

PQ = R + r = 7 cm

Question 10: A man starting at a point walks one km east, then two km north, then one km east, then one km north, then one km east and then one km north to arrive at the destination. What is the shortest distance from the starting point to the destination?

a) $2\sqrt{2}$ km

b) $7$ km

c) $3\sqrt{2}$ km

d) $5$ km

10) Answer (D)

View Video Solution

Solution:

In the diagram, A is starting point and B is ending point.
Accordingly, AB = $\sqrt{(3^2 + 4^2)} = 5$

Question 11: In triangleABC, ∠B is a right angle, AC = 6 cm, and D is the mid-point of AC. The length of BD is

a) 4cm

b) 6 cm

c) 3cm

d) 3.5cm

11) Answer (C)

View Video Solution

Solution:

A circle is circumscribed to triangle ABC.

For this circle D will be centre of circle, and AD , DC , BD will radius of this circle.

Hence AD=BD=DC=3 cm

Question 12: In ABC, points P, Q and R are the mid-points of sides AB, BC and CA respectively. If area of ABC is 20 sq. units, find the area of PQR.

a) 10 sq. units

b) 5√3 sq. units

c) 5 sq. units

d) None of these

12) Answer (C)

View Video Solution

Solution:

As we know, the triangle joining midpoints of sides will divide it in 4 similar traingles of equal area.

So area will be = $\frac{20}{4} = 5$

Question 13: Four identical coins are placed in a square. For each coin the ratio of area to circumference is same as the ratio of circumference to area. Then find the area of the square that is not covered by the coins.

a) 16(π – 1)

b) 16(8 – π)

c) 16(4 – π)

d) 16 $(4- \frac{\pi}{2})$

13) Answer (C)

View Video Solution

Solution:

$\frac{(\pi r^2)}{2 \pi r}$ = $\frac{2 \pi r}{ \pi r^2}$
So r = 2
Hence required area = (Area of square) – (Area of 4 circles)
= $(8^2) – (4 \pi (2^2))$ (As side of square will be 4*2 = 8)
= $16 (4- \pi)$

The intended diagram can be drawn as follows:

ABCD is the square and the coins are placed (numbered 1,2,3,4)

Question 14: Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is

14) Answer: 24

View Video Solution

Solution:

The length of the altitude from A to the hypotenuse will be the shortest distance.

This is a right triangle with sides 3 : 4 : 5.

Hence, the hypotenuse = $\sqrt{20^2+15^2}$ = 25 Km.

Length of the altitude = $\frac{15 * 20}{25}$ = 12 Km

(This is derived from equating area of triangle, $\frac{15\cdot20}{2}\ =\ \frac{25\cdot\text{altitude}}{2}$)

The time taken = $\frac{12}{30} * 60$ = 24 minutes

Question 15: A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is

a) $5\sqrt{3}$

b) $2\pi$

c) $8$

d) $6\sqrt{2}$

15) Answer (A)

View Video Solution

Solution:

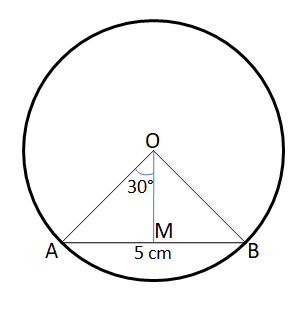
We are given that AB = 5 cm and $\angle$ AOB = 60°

Let us draw OM such that OM $\perp$ AB.

In right angle triangle AMO,

$sin 30° = \dfrac{AM}{AO}$

$\Rightarrow$ AO = 2*AM = 2*2.5 = 5 cm. Therefore, we can say that the radius of the circle = 5 cm.

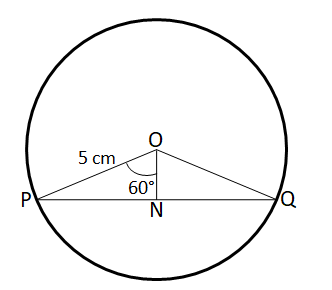
In right angle triangle PNO,

$sin 60° = \dfrac{PN}{PO}$

$\Rightarrow$ PN = $\dfrac{\sqrt{3}}{2}$*PO = $\dfrac{5\sqrt{3}}{2}$

Therefore, PQ = 2*PN = $5\sqrt{3}$ cm

Question 16: A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is

a) $1026(1 + \pi)$

b) $8464\pi$

c) $928\pi$

d) $1044(4 + \pi)$

16) Answer (A)

View Video Solution

Solution:

It is given that the volume of all the cylinders is the same, so the volume of each cylinder = HCF of (405, 783, 351)

=27

The number of iron cylinders = $\ \frac{\ 405}{27}$ = 15

The number of aluminium cylinders = $\ \frac{\ 783}{27}$ = 29

The number of copper cylinders = $\ \frac{351\ }{27}$ = 13

15*$\pi\ r^2h=$ 405

15*$\pi\ 9*h=$ 405

$\pi\ h=3$

Now we have to calculate the total surface area of all the cylinders

Total number of cylinders = 15+29+13 = 57

Total surface area of the cylinder = 57*($2\pi\ rh+2\pi\ r^2$)

=57(2*3*3 + 2*9*$\pi\ $)

=$1026(1 + \pi)$

Question 17: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is

a) $\frac{14\pi}{3}$

b) $\frac{123\pi}{7}$

c) $\frac{12\pi}{5}$

d) $\frac{205\pi}{9}$

17) Answer (D)

View Video Solution

Solution:

Equation of circle $x^2+y^2+2gx+2fy+c=0$

It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:

=> On substituting the value (0,0) in the above equation, we obtain: $c=0$

=> On substituting the value (4,0) in the above equation, we obtain:  $16+0+8g+0 = 0$ ; $g=-2$

=> On substituting the value (3,9) in the above equation, we obtain: $9+81-12+18f = 0$ ; $f= -13/3$

Radius of the circle r = $\sqrt{\ g^2+f^2-c}$ => $r^2=\frac{205}{9}$

Therefore, Area = $\pi\ r^2=\frac{205\pi\ }{9}$

Question 18: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

a) 30

b) 40

c) 25

d) 20

18) Answer (A)

View Video Solution

Solution:

We are given that :

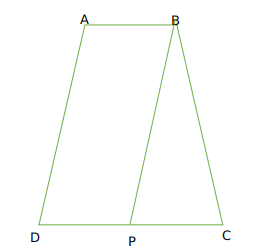
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$\frac{1}{2}xh$
Now by condition$xh-\frac{1}{2}xh=10$
$\frac{xh}{2}=10$
so xh =20
Now therefore area of trapezium ABCD = $\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$

Question 19: Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle $\angle ADC$ is equal to $30^{0}$ then the area of the parallelogram, in sq.cm is

a) $\frac{25(\sqrt{5}+\sqrt{15})}{2}$

b) $25(\sqrt{3}+\sqrt{15})$

c) $\frac{25(\sqrt{3}+\sqrt{15})}{2}$

d) ${25(\sqrt{5}+\sqrt{15})}$

19) Answer (B)

View Video Solution

Solution:

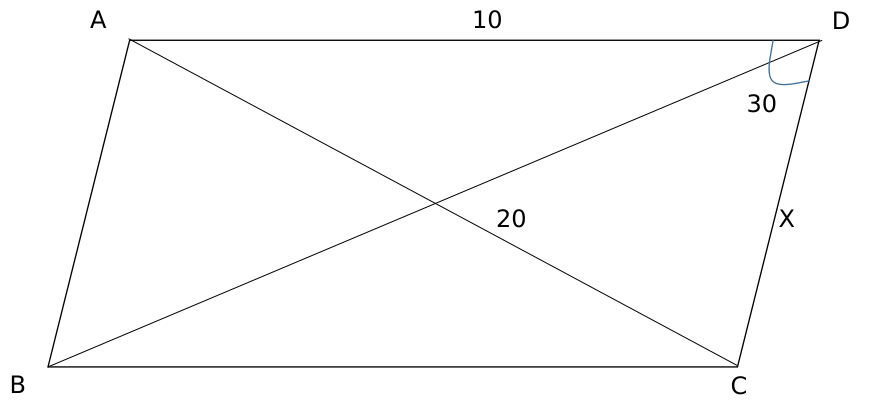
Applying cosine rule in triangle ACD,

$100+X^2-2\times\ 10\times\ X\cos30=400$

$X^2-10X\sqrt{\ 3}-300=0$

Solving, we get X = $\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)$

Hence, area = 10Xsin 30 = $\frac{\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)10}{2}$

= $25(\sqrt{3}+\sqrt{15})$

Question 20: In a triangle ABC, AB = AC = 8 cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through Band C. Then the area, in sq. cm, of the overlapping region between the two circles is

a) $16\pi$

b) $16(\pi – 1)$

c) $32(\pi – 1)$

d) $32\pi$

20) Answer (C)

View Video Solution

Solution:

BC is the diameter of circle C2 so we can say that $\angle BAC=90^{\circ\ }$ as angle in the semi circle is $90^{\circ\ }$

Therefore overlapping area = $\frac{1}{2}$(Area of circle C2) + Area of the minor sector made be BC in C1

AB= AC = 8 cm and as $\angle BAC=90^{\circ\ }$, so we can conclude that BC= $8\sqrt{2}$ cm

Radius of C2 = Half of length of BC = $4\sqrt{2}$ cm

Area of C2 = $\pi\left(4\sqrt{2}\right)^2=32\pi$ $cm^2$

A is the centre of C1 and C1 passes through B, so AB is the radius of C1 and is equal to 8 cm

Area of the minor sector made be BC in C1 = $\frac{1}{4}$(Area of circle C1) – Area of triangle ABC = $\frac{1}{4}\pi\left(8\right)^2-\left(\frac{1}{2}\times8\times8\right)=16\pi-32$ $cm^2$

Therefore,

Overlapping area between the two circles= $\frac{1}{2}$(Area of circle C2) + Area of the minor sector made be BC in C1

= $\frac{1}{2}\left(32\pi\right)\ +\left(16\pi-32\right)=32\left(\pi-1\right)$ $cm^2$