CAT Quadratic Equations Questions PDF [Important]

Quadratic Equations is an important topic in the CAT Quants Section. Quadratic Equation questions are not very difficult if you learn the basics and practice them well. Questions on Quadratic Equations are asked frequently in the CAT. You can expect 1-2 questions from Quadratic Equations in the latest format of the CAT Quants section. This article will look into some important Quadratic Equation Questions for CAT QA section. If you want to practice these important Quadratic Equation questions, you can download the PDF, which is completely Free.

Download Quadratic Equation Questions for CAT

Enroll for CAT 2022 Crash Course

Question 1: A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is

a) 175

b) 150

c) 200

d) 225

1) Answer (C)

View Video Solution

Solution:

Let the number of large shirts be l and the number of small shirts be s.

Let the price of a small shirt be x and that of a large shirt be x + 50.

Now, s + l = 64

l (x+50) = 5000

sx = 1800

Adding them, we get,

lx + sx + 50l = 6800

64x +50l = 6800

Substituting l = (6800 – 64x) / 50, in the original equation, we get

$\frac{\left(6800-64x\right)}{50}\left(x+50\right)=5000$

(6800 – 64x)(x + 50) = 250000

$6800x+340000-64x^2-3200x = 250000$

$64x^2-3600x-90000=0$

Solving, we get, x= $\frac{225\pm\ 375}{8}=\frac{600}{8}or-\frac{150}{8}$

SO, x = 75

x + 50 = 125

Answer = 75 + 125 = 200.

Alternate approach: By options.

Hint: Each option gives the sum of the costs of one large and one small shirt. We know that large = small + 50

Hence, small + small + 50 = option.

SMALL = (Option – 50)/2

LARGE = Small + 50 = (Option + 50)/2

Option A and Option D gives us decimal values for SMALL and LARGE, hence we will consider them later.

Lets start with Option B.

Large = 150 + 50 / 2 = 100

Small = 150 – 50 / 2 = 50

Now, total shirts = 5000/100 + 1800/50 = 50 + 36 = 86 (X – This is wrong)

Option C –

Large = 200 + 50 / 2 = 125

Small = 200 – 50 / 2 = 75

Total shirts = 5000/125 + 1800/75 = 40 + 24 = 64 ( This is the right answer)

Question 2: Consider the pair of equations: $x^{2}-xy-x=22$ and $y^{2}-xy+y=34$. If $x>y$, then $x-y$ equals

a) 6

b) 4

c) 7

d) 8

2) Answer (D)

View Video Solution

Solution:

We have :
$x^2-xy-x\ =22\ \ \ \ \ \ \left(1\right)$
And $y^2-xy+y\ =34\ \ \ \ \ \ \left(1\right)$               (2)
Adding (1) and (2)
we get $x^2-2xy+y^2-x+y\ =56$
we get $\left(x-y\right)^2-\ \left(x-y\right)\ =56$
Let (x-y) =t
we get $t^2-t=56$
$t^2-t-56=0$
(t-8)(t+7) =0
so t=8
so x-y =8

Question 3: For all real values of x, the range of the function $f(x)=\frac{x^{2}+2x+4}{2x^{2}+4x+9}$ is:

a) $[\frac{4}{9},\frac{8}{9}]$

b) $[\frac{3}{7},\frac{8}{9})$

c) $(\frac{3}{7},\frac{1}{2})$

d) $[\frac{3}{7},\frac{1}{2})$

3) Answer (D)

View Video Solution

Solution:

$f(x)=\frac{x^{2}+2x+4}{2x^{2}+4x+9}$

If we closely observe the coefficients of the terms in the numerator and denominator, we see that the coefficients of the $x^2$ and x in the numerators are in ratios 1:2. This gives us a hint that we might need to adjust the numerator to decrease the number of variables.

$f(x)=\frac{x^2+2x+4}{2x^2+4x+9}=\frac{x^2+2x+4.5-0.5}{2x^2+4x+9}$

= $\frac{x^2+2x+4.5}{2x^2+4x+9}-\frac{0.5}{2x^2+4x+9}$

= $\frac{1}{2}-\frac{0.5}{2x^2+4x+9}$

Now, we only have terms of x in the denominator.

The maximum value of the expression is achieved when the quadratic expression $2x^2+4x+9$ achieves its highest value, that is infinity.

In that case, the second term becomes zero and the expression becomes 1/2. However, at infinity, there is always an open bracket ‘)’.

To obtain the minimum value, we need to find the minimum possible value of the quadratic expression.

The minimum value is obtained when 4x + 4 = 0 [d/dx = 0]

x=-1.

The expression comes as 7.

The entire expression becomes 3/7.

Hence, $[\frac{3}{7},\frac{1}{2})$

Question 4: Suppose one of the roots of the equation $ax^{2}-bx+c=0$ is $2+\sqrt{3}$, Where a,b and c are rational numbers and $a\neq0$. If $b=c^{3}$ then $\mid a\mid$ equals.

a) 1

b) 2

c) 3

d) 4

4) Answer (B)

View Video Solution

Solution:

Given a, b, c are rational numbers.

Hence a, b, c are three numbers that can be written in the form of p/q.

Hence if one both the root is 2+$\sqrt{\ 3}$ and considering the other root to be x.

The sum of the roots and the product of the two roots must be rational numbers.

For this to happen the other root must be the conjugate of $2+\sqrt{\ 3}$ so the product and the sum of the roots are rational numbers which are represented by: $\frac{b}{a},\ \frac{c}{a}$

Hence the sum of the roots is 2+$\sqrt{\ 3}+2-\sqrt{\ 3}$ = 4.

The product of the roots is $\left(2+\sqrt{\ 3}\right)\cdot\left(2-\sqrt{\ 3}\right)\ =\ 1$

b/a = 4, c/a = 1.

b = 4*a, c= a.

Since b = $c^3$

4*a = $a^3$

$a^2=\ 4.$

a = 2 or -2.

|a| = 2

Question 5: If r is a constant such that $\mid x^2 – 4x – 13 \mid = r$ has exactly three distinct real roots, then the value of r is

a) 17

b) 21

c) 15

d) 18

5) Answer (A)

View Video Solution

Solution:

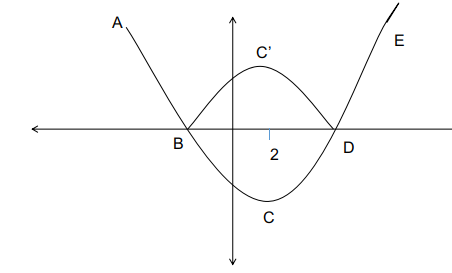
The quadratic equation of the form $\mid x^2 – 4x – 13 \mid = r$ has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.

Hence at x = 2 the quadratic equation has its minimum.

Considering the quadratic part : $\left|x^2-4\cdot x-13\right|$. as per the given condition, this must-have 3 real roots.

The curve ABCDE represents the function $\left|x^2-4\cdot x-13\right|$. Because of the modulus function, the representation of the quadratic equation becomes :

ABC’DE.

There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C’.

The point C’ is a reflection of C about the x-axis. r is the y coordinate of the point C’ :

The point C which is the value of the function at x = 2, = $2^2-8-13$

= -17, the reflection about the x-axis is 17.

Alternatively,

$\mid x^2 – 4x – 13 \mid = r$ .

This can represented in two parts :

$x^2-4x-13\ =\ r\ if\ r\ is\ positive.$

$x^2-4x-13\ =\ -r\ if\ r\ is\ negative.$

Considering the first case : $x^2-4x-13\ =r$

The quadraticequation becomes : $x^2-4x-13-r\ =\ 0$

The discriminant for this function is : $b^2-4ac\ =\ 16-\ \left(4\cdot\left(-13-r\right)\right)=68+4r$

SInce r is positive the discriminant is always greater than 0 this must have two distinct roots.

For the second case :

$x^2-4x-13+r\ =\ 0$ the function inside the modulus is negaitve

The discriminant is $16\ -\ \left(4\cdot\left(r-13\right)\right)\ =\ 68-4r$

In order to have a total of 3 roots, the discriminant must be equal to zero for this quadratic equation to have a total of 3 roots.

Hence $\ 68-4r\ =\ 0$

r = 17, for r = 17 we can have exactly 3 roots.

Question 6: Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was

6) Answer: 35

View Video Solution

Solution:

Let the number of Covid patients in Hospitals A and B be x and x+21 respectively. Then, it has been given that:

$\frac{200}{x}-\frac{152}{x+21}=3$

$\frac{\left(200x+4200-152x\right)}{x\left(x+21\right)}=3$

$\frac{\left(48x+4200\right)}{x\left(x+21\right)}=3$

$16x+1400=x\left(x+21\right)$

$x^2+5x-1400=0$

(x+40)(x-35)=0

Hence, x=35.

Checkout: CAT Free Practice Questions and Videos

Question 7: The number of integers that satisfy the equality $(x^{2}-5x+7)^{x+1}=1$ is

a) 3

b) 2

c) 4

d) 5

7) Answer (A)

View Video Solution

Solution:

$\left(x^2-5x+7\right)^{x+1}=1$

There can be a solution when $\left(x^2-5x+7\right)=1$ or $x^2-5x\ +6=0$

or x=3 and x=2

There can also be a solution when x+1 = 0 or x=-1

Hence three possible solutions exist.

Question 8: Let m and n be positive integers, If $x^{2}+mx+2n=0$ and $x^{2}+2nx+m=0$ have real roots, then the smallest possible value of $m+n$ is

a) 7

b) 6

c) 8

d) 5

8) Answer (B)

View Video Solution

Solution:

To have real roots the discriminant should be greater than or equal to 0.

So, $m^2-8n\ge0\ \&\ 4n^2-4m\ge0$

=> $m^2\ge8n\ \&\ n^2\ge m$

Since m,n are positive integers the value of m+n will be minimum when m=4 and n=2.

.’. m+n=6.

Question 9: The number of distinct real roots of the equation $(x+\frac{1}{x})^{2}-3(x+\frac{1}{x})+2=0$ equals

9) Answer: 1

View Video Solution

Solution:

Let $a=x+\frac{1}{x}$
So, the given equation is $a^2-3a+2=0$
So, $a$ can be either 2 or 1.

If $a=1$, $x+\frac{1}{x}=1$ and it has no real roots.
If $a=2$, $x+\frac{1}{x}=2$ and it has exactly one real root which is $x=1$

So, the total number of distinct real roots of the given equation is 1

Question 10: How many disticnt positive integer-valued solutions exist to the equation $(x^{2}-7x+11)^{(x^{2}-13x+42)}=1$ ?

a) 8

b) 4

c) 2

d) 6

10) Answer (D)

View Video Solution

Solution:

$(x^{2}-7x+11)^{(x^{2}-13x+42)}=1$

if $(x^{2}-13x+42)$=0 or $(x^{2}-7x+11)$=1 or $(x^{2}-7x+11)$=-1 and $(x^{2}-13x+42)$ is even number

For x=6,7 the value $(x^{2}-13x+42)$=0

$(x^{2}-7x+11)$=1 for x=5,2.

$(x^{2}-7x+11)$=-1 for x=3,4 and for X=3 or 4, $(x^{2}-13x+42)$ is even number.

.’. {2,3,4,5,6,7} is the solution set of x.

.’. x can take six values.

Question 11: The number of solutions to the equation $\mid x \mid (6x^2 + 1) = 5x^2$ is

11) Answer: 5

View Video Solution

Solution:

For x <0, -x($6x^2+1$) = $5x^2$

=> ($6x^2+1$) = -5x

=> ($6x^2 + 5x+ 1$) = 0

=>($6x^2 + 3x+2x+ 1$) = 0

=> (3x+1)(2x+1)=0    =>x=$\ -\frac{\ 1}{3}$  or x=$\ -\frac{\ 1}{2}$

For x=0, LHS=RHS=0    (Hence, 1 solution)

For x >0, x($6x^2+1$) = $5x^2$

=> ($6x^2 – 5x+ 1$) = 0

=>(3x-1)(2x-1)=0    =>x=$\ \frac{\ 1}{3}$   or   x=$\ \frac{\ 1}{2}$

Hence, the total number of solutions = 5

Question 12: The product of the distinct roots of $\mid x^2 – x – 6 \mid = x + 2$ is

a) −16

b) -4

c) -24

d) -8

12) Answer (A)

View Video Solution

Solution:

We have, $\mid x^2 – x – 6 \mid = x + 2$

=> |(x-3)(x+2)|=x+2

For x<-2, (3-x)(-x-2)=x+2

=> x-3=1   =>x=4 (Rejected as x<-2)

For -2$\le\ $x<3, (3-x)(x+2)=x+2    =>x=2,-2

For x$\ge\ $3, (x-3)(x+2)=x+2   =>x=4

Hence the product =4*-2*2=-16

Question 13: The quadratic equation $x^2 + bx + c = 0$ has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of $b^2 + c$?

a) 3721

b) 361

c) 427

d) 549

13) Answer (D)

View Video Solution

Solution:

Given,

The quadratic equation $x^2 + bx + c = 0$ has two roots 4a and 3a

7a=-b

12$a^2$ = c

We have to find the value of  $b^2 + c$ = 49$a^2$+ 12$a^2$=61$a^2$

Now lets verify the options

61$a^2$ = 3721 ==> a= 7.8 which is not an integer

61$a^2$ = 361 ==> a= 2.42 which is not an integer

61$a^2$ = 427 ==> a= 2.64 which is not an integer

61$a^2$ = 3721 ==> a= 3 which is an integer

Question 14: Let A be a real number. Then the roots of the equation $x^2 – 4x – log_{2}{A} = 0$ are real and distinct if and only if

a) $A > \frac{1}{16}$

b) $A < \frac{1}{16}$

c) $A < \frac{1}{8}$

d) $A > \frac{1}{8}$

14) Answer (A)

View Video Solution

Solution:

The roots of $x^2 – 4x – log_{2}{A} = 0$ will be real and distinct if and only if the discriminant is greater than zero

16+4*$log_{2}{A}$ > 0

$log_{2}{A}$ > -4

A> 1/16

Question 15: If a and b are integers such that $2x^2−ax+2>0$ and $x^2−bx+8≥0$ for all real numbers $x$, then the largest possible value of $2a−6b$ is

15) Answer: 36

View Video Solution

Solution:

Let f(x) = $2x^2−ax+2$. We can see that f(x) is a quadratic function.

For, f(x) > 0, Discriminant (D) < 0

$\Rightarrow$ $(-a)^2-4*2*2<0$

$\Rightarrow$ (a-4)(a+4)<0

$\Rightarrow$ a $\epsilon$ (-4, 4)

Therefore, integer values that ‘a’ can take = {-3, -2, -1, 0, 1, 2, 3}

Let g(x) = $x^2−bx+8$. We can see that g(x) is also a quadratic function.

For, g(x)≥0, Discriminant (D) $\leq$ 0

$\Rightarrow$ $(-b)^2-4*8*1<0$

$\Rightarrow$ $(b-\sqrt{32})(b+\sqrt{32})<0$

$\Rightarrow$ b $\epsilon$ (-$\sqrt{32}$, $\sqrt{32}$)

Therefore, integer values that ‘b’ can take = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}

We have to find out the largest possible value of $2a−6b$. The largest possible value will occur when ‘a’ is maximum and ‘b’ is minimum.

a$_{max}$ = 3, b$_{min}$ = -5

Therefore, the largest possible value of $2a−6b$ = 2*3 – 6*(-5) = 36.