The Logical Reasoning and Data Interpretation (LRDI) section in the CAT Exam is often a deciding factor for many students. Neglecting this section could prove costly and, thus, requires thorough preparation. If you’re new to this section, you can check out these CAT LRDI Questions from the CAT previous year papers. This article provides essential LRDI questions in PDF format, complete with solutions and crucial tips for solving them. These CAT LRDI questions are also available for download, including detailed solutions and tricks to aid in solving these questions effectively.
Download LRDI Questions for CAT
Instructions
Mathematicians are assigned a number called Erdos number (named after the famous mathematician, Paul Erdos). Only Paul Erdos himself has an Erdos number of zero. Any mathematician who has written a research paper with Erdos has an Erdos number of 1.For other mathematicians, the calculation of his/her Erdos number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. ‘From among them, mathematician Y has the smallest Erdos number. Let the Erdos number of Y be y. Then X has an Erdos number of y+1. Hence any mathematician with no co-authorship chain connected to Erdos has an Erdos number of infinity. :
In a seven day long mini-conference organized in memory of Paul Erdos, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdos number. Nobody had an Erdos number less than that of F.
On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdos number of the group of eight mathematicians to 3. The Erdos numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdos number of the group of eight to as low as 3.
• At the end of the third day, five members of this group had identical Erdos numbers while the other three had Erdos numbers distinct from each other.
• On the fifth day, E co-authored a paper with F which reduced the group’s average Erdos number by 0.5. The Erdos numbers of the remaining six were unchanged with the writing of this paper.
• No other paper was written during the conference.
Question 1: The person having the largest Erdos number at the end of the conference must have had Erdos number (at that time):
a) 5
b) 7
c) 9
d) 14
e) 15
1) Answer (B)
Solution:
Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.
At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same. [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]
Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24
Erdos number at the third day:f+1,b,f+1,d,e,f,g,h
At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.
So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h
At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.
It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.
So five mathematicians will have f+1, one with f+5,one with f, one with some different value say x
5(f+1)+f+5+f+x=24
7f+x=14
The only value which satisfies the above equation is f=1,x=7
Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence the person having the largest Erdos number at the end of the conference must have had Erdos number 7 . Hence option B.
Question 2: How many participants in the conference did not change their Erdos number during the conference?
a) 2
b) 3
c) 4
d) 5
e) Cannot be determined
2) Answer (D)
Solution:
Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.
At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same. [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]
Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24
Erdos number at the third day:f+1,b,f+1,d,e,f,g,h
At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.
So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h
At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.
It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.
So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x
5(f+1)+f+5+f+x=24
7f+x=14
The only value which satisfies the above equation is f=1,x=7
Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

So B,D ,F,G,H are 5 participants in the conference who did not change their Erdos number during the conference.
Question 3: The Erdos number of C at the end of the conference was:
a) 1
b) 2
c) 3
d) 4
e) 5
3) Answer (B)
Solution:
Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.
At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same. [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]
Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24
Erdos number at the third day:f+1,b,f+1,d,e,f,g,h
At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.
So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h
At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.
It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.
So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x
5(f+1)+f+5+f+x=24
7f+x=14
The only value which satisfies the above equation is f=1,x=7
Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Erdos no. of C at the end is f+1 = 1+1 = 2. Hence option B.
Question 4: The Erdos number of E at the beginning of the conference was:
a) 2
b) 5
c) 6
d) 7
e) 8
4) Answer (C)
Solution:
Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.
At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same. [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]
Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24
Erdos number at the third day:f+1,b,f+1,d,e,f,g,h
At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.
So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h
At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.
It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.
So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x
5(f+1)+f+5+f+x=24
7f+x=14
The only value which satisfies the above equation is f=1,x=7
Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence erdos no. of E at the beginning of conference would be f+5 = 6 .
Question 5: How many participants had the same Erdos number at the beginning of the conference?
a) 2
b) 3
c) 4
d) 5
e) Cannot be determined
5) Answer (B)
Solution:

Since at the end of the 3rd day 5 people had identical erdos no.(f+1) so : 5*(f+1) +f+f+5+x = 24 ; Only f=1 and x = 7 satisfies the equation. So out of 5 people who had identical erdos no. at the end of day 3, 2 of them had different nos. at the beginning. So there were 5-2 = 3 participants who had the same Erdos number at the beginning of the conference.
Instructions
Each visitor to an amusement park needs to buy a ticket. Tickets can be Platinum, Gold, or Economy. Visitors are classified as Old, Middle-aged, or Young. The following facts are known about visitors and ticket sales on a particular day:
1. 140 tickets were sold.
2. The number of Middle-aged visitors was twice the number of Old visitors, while the number of Young visitors was twice the number of Middle-aged visitors.
3. Young visitors bought 38 of the 55 Economy tickets that were sold, and they bought half the total number of Platinum tickets that were sold.
4. The number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
Question 6: If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Platinum tickets, then which among the following could be the total number of Platinum tickets sold?
a) 34
b) 36
c) 38
d) 32
6) Answer (D)
Solution:
Let ‘x’ be the the number of Old visitors. Then, the number of middle-aged visitors = 2x.
Also, the number of Young visitors = 2*2x = 4x
$\Rightarrow$ x+2x+4x = 140
$\Rightarrow$ x = 20
It is given that total of 55 Economy tickets were sold out.
It is given that Young visitors half the total number of Platinum tickets that were sold.
Let ‘Y’ be the number of Platinum tickets bought by the Young visitors.
Then,the number of Platinum tickets sold = 2Y.
Consequently, we can say that the number of Gold tickets sold = 140 – 55 – 2Y = 85 – 2Y.
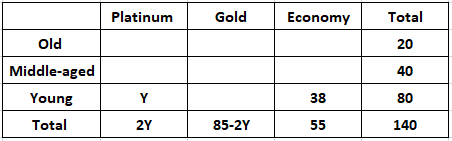
Let us assume that ‘Z’ is the number of Economy tickets bought by the Old visitors. It is given that the number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.
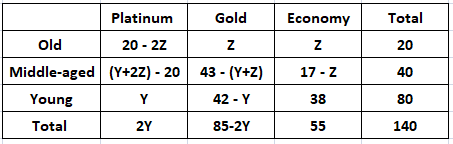
It is given that the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Platinum tickets.
20 – 2Z = (Y+2Z) – 20
Y + 4Z = 40
2Y + 8Z = 80
2Y = 80 – 8Z
We can see that Z can take only integer values. Therefore, we can say that the the total number of Platinum tickets sold will be a multiple of 8. Hence, option D is the correct answer.
Question 7: If the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Economy tickets, then the number of Old visitors buying Gold tickets was
7) Answer: 3
Solution:
Let ‘x’ be the the number of Old visitors. Then, the number of middle-aged visitors = 2x.
Also, the number of Young visitors = 2*2x = 4x
$\Rightarrow$ x+2x+4x = 140
$\Rightarrow$ x = 20
It is given that total of 55 Economy tickets were sold out.
It is given that Young visitors half the total number of Platinum tickets that were sold.
Let ‘Y’ be the number of Platinum tickets bought by the Young visitors.
Then,the number of Platinum tickets sold = 2Y.
Consequently, we can say that the number of Gold tickets sold = 140 – 55 – 2Y = 85 – 2Y.

Let us assume that ‘Z’ is the number of Economy tickets bought by the Old visitors. It is given that the number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.

It is given that the number of Old visitors buying Platinum tickets was equal to the number of Middle-aged visitors buying Economy tickets.
20 – 2Z = 17 – Z
$\Rightarrow$ Z = 3
Therefore, we can say that the number of Old visitors buying Gold tickets = 3
Question 8: If the number of Old visitors buying Gold tickets was strictly greater than the number of Young visitors buying Gold tickets, then the number of Middle-aged visitors buying Gold tickets was
8) Answer: 0
Solution:
Let ‘x’ be the the number of Old visitors. Then, the number of middle-aged visitors = 2x.
Also, the number of Young visitors = 2*2x = 4x
$\Rightarrow$ x+2x+4x = 140
$\Rightarrow$ x = 20
It is given that total of 55 Economy tickets were sold out.
It is given that Young visitors half the total number of Platinum tickets that were sold.
Let ‘Y’ be the number of Platinum tickets bought by the Young visitors.
Then,the number of Platinum tickets sold = 2Y.
Consequently, we can say that the number of Gold tickets sold = 140 – 55 – 2Y = 85 – 2Y.

Let us assume that ‘Z’ is the number of Economy tickets bought by the Old visitors. It is given that the number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.

It is given that the number of Old visitors buying Gold tickets was strictly greater than the number of Young visitors buying Gold tickets.
Z > 42 – Y
$\Rightarrow$ Z + Y > 42 … (1)
The number of Middle-aged visitors buying Gold tickets = 43 – (Y+Z)
Since (Y+Z) > 42, then We can say that (Y+Z)$_{min}$ = 43.
Hence, the number of Middle-aged visitors buying Gold tickets = 43 – 43 = 0
Checkout: CAT Free Practice Questions and Videos
Question 9: Which of the following statements MUST be FALSE?
a) The numbers of Gold and Platinum tickets bought by Young visitors were equal
b) The numbers of Middle-aged and Young visitors buying Gold tickets were equal
c) The numbers of Old and Middle-aged visitors buying Platinum tickets were equal
d) The numbers of Old and Middle-aged visitors buying Economy tickets were equal
9) Answer (D)
Solution:
Let ‘x’ be the the number of Old visitors. Then, the number of middle-aged visitors = 2x.
Also, the number of Young visitors = 2*2x = 4x
$\Rightarrow$ x+2x+4x = 140
$\Rightarrow$ x = 20
It is given that total of 55 Economy tickets were sold out.
It is given that Young visitors half the total number of Platinum tickets that were sold.
Let ‘Y’ be the number of Platinum tickets bought by the Young visitors.
Then,the number of Platinum tickets sold = 2Y.
Consequently, we can say that the number of Gold tickets sold = 140 – 55 – 2Y = 85 – 2Y.

Let us assume that ‘Z’ is the number of Economy tickets bought by the Old visitors. It is given that the number of Gold tickets bought by Old visitors was equal to the number of Economy tickets bought by Old visitors.

Let us check with the help of options.
Option (A): The numbers of Gold and Platinum tickets bought by Young visitors were equal.
Y = 42 – Y
$\Rightarrow$ Y = 21. Hence, this statement can be true.
Option (B): The numbers of Middle-aged and Young visitors buying Gold tickets were equal
43 – (Y+Z) = 42 – Y
$\Rightarrow$ Z = 1. Hence, this statement can be true.
Option (C): The numbers of Old and Middle-aged visitors buying Platinum tickets were equal
20 – 2Z = (Y+2Z) – 20
$\Rightarrow$ Y+4Z = 40. Hence, this statement can be true.
Option (D): The numbers of Old and Middle-aged visitors buying Economy tickets were equal
Z = 17 – Z
$\Rightarrow$ Z = 8.5. This is not possible as Z has to be an integer. Hence, we can say that this statement is false.
LRDI Videos | Preparation Videos for CAT LRDI
- Try these 3 Cracku Free CAT Mocks, which come with detailed solutions and with video explanations.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
