Games and Tournaments is one of the most important topics in the CAT Logical Reasoning & Data Interpretation (LRDI) section. These questions are not very tough if you understand the concept. Know all the Key Concepts from Games & Tournaments. Solve & practice more sets from CAT Games and Tournaments so that you get a hang of these kinds of sets. You can check out these CAT Games and Tournaments questions from the CAT Previous year papers. In this post, we will look into some important Games and Tournaments LRDI Sets for CAT. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download these Important Games and Tournaments (LRDI) Questions for CAT PDF (with detailed answers) along with the video solutions below, which are completely Free.
Download Games and Tournaments (LRDI) Questions for CAT
Enroll for CAT 2022 Online Course
Instructions
Ten players, as listed in the table below, participated in a rifle shooting competition comprising of 10 rounds. Each round had 6 participants. Players numbered 1 through 6 participated in Round 1, players 2 through 7 in Round 2,…, players 5 through 10 in Round 5, players 6 through 10 and 1 in Round 6, players 7 through 10, 1 and 2 in Round 7 and so on. The top three performances in each round were awarded 7, 3 and 1 points respectively. There were no ties in any of the 10 rounds. The table below gives the total number of points obtained by the 10 players after Round 6 and Round 10.
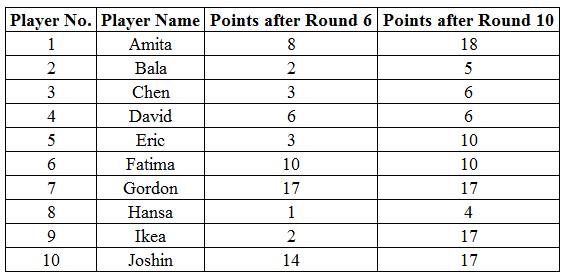
The following information is known about Rounds 1 through 6:
1. Gordon did not score consecutively in any two rounds.
2. Eric and Fatima both scored in a round.
The following information is known about Rounds 7 through 10:
1. Only two players scored in three consecutive rounds. One of them was Chen. No other player scored in any two consecutive rounds.
2. Joshin scored in Round 7, while Amita scored in Round 10.
3. No player scored in all the four rounds.
Question 1: What were the scores of Chen, David, and Eric respectively after Round 3?
a) 3, 6, 3
b) 3, 3, 3
c) 3, 3, 0
d) 3, 0, 3
1) Answer (B)
Solution:
From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.
By observing the table:
1. Jordan(J) scored 7 points in both the rounds 5th & 6th.
2. Amita (A) scored 1,7 points then she scored 7 in the first round.
3. Bala (B) scored 1 point in both the rounds 1st and 2nd.
4. Ikea (I) scored 1 point in the round 4th and 5th.
5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2nd, 4th and 6th rounds respectively.
We can make the following table from the details given in the question.
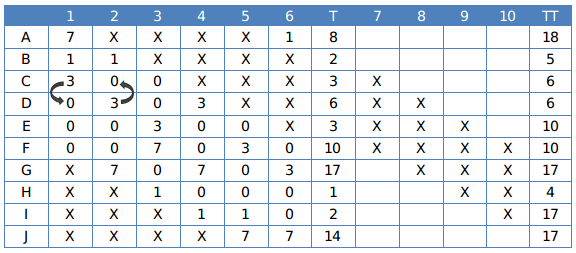
T: Total after the sixth round and TT: Total after the 10th round.
1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.
2. Ikea scored 15 points (1,7,7) in three rounds respectively.
3. Eric scored 7 in round 10.
4. Amita will score 3 in round 10, and 7 in round 7.
We can make the following table:

Hence option B is correct.
Question 2: Which three players were in the last three positions after Round 4?
a) Bala, Ikea, Joshin
b) Bala, Hansa, Ikea
c) Bala, Chen, Gordon
d) Hansa, Ikea, Joshin
2) Answer (D)
Solution:
From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.
By observing the table:
1. Jordan(J) scored 7 points in both the rounds 5th & 6th.
2. Amita (A) scored 1,7 points then she scored 7 in the first round.
3. Bala (B) scored 1 point in both the rounds 1st and 2nd.
4. Ikea (I) scored 1 point in the round 4th and 5th.
5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2nd, 4th and 6th rounds respectively.
We can make the following table from the details given in the question.

T: Total after the sixth round and TT: Total after the 10th round.
1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.
2. Ikea scored 15 points (1,7,7) in three rounds respectively.
3. Eric scored 7 in round 10.
4. Amita will score 3 in round 10, and 7 in round 7.
We can make the following table:

Hence option D is correct.
Question 3: Which player scored points in maximum number of rounds?
a) Joshin
b) Chen
c) Amita
d) Ikea
3) Answer (D)
Solution:
From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.
By observing the table:
1. Jordan(J) scored 7 points in both the rounds 5th & 6th.
2. Amita (A) scored 1,7 points then she scored 7 in the first round.
3. Bala (B) scored 1 point in both the rounds 1st and 2nd.
4. Ikea (I) scored 1 point in the round 4th and 5th.
5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2nd, 4th and 6th rounds respectively.
We can make the following table from the details given in the question.

T: Total after the sixth round and TT: Total after the 10th round.
1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.
2. Ikea scored 15 points (1,7,7) in three rounds respectively.
3. Eric scored 7 in round 10.
4. Amita will score 3 in round 10, and 7 in round 7.
We can make the following table:

Hence option D is correct.
Question 4: Which players scored points in the last round?
a) Amita, Eric, Joshin
b) Amita, Chen, David
c) Amita, Bala, Chen
d) Amita, Chen, Eric
4) Answer (D)
Solution:
From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.
By observing the table:
1. Jordan(J) scored 7 points in both the rounds 5th & 6th.
2. Amita (A) scored 1,7 points then she scored 7 in the first round.
3. Bala (B) scored 1 point in both the rounds 1st and 2nd.
4. Ikea (I) scored 1 point in the round 4th and 5th.
5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2nd, 4th and 6th rounds respectively.
We can make the following table from the details given in the question.

T: Total after the sixth round and TT: Total after the 10th round.
1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.
2. Ikea scored 15 points (1,7,7) in three rounds respectively.
3. Eric scored 7 in round 10.
4. Amita will score 3 in round 10, and 7 in round 7.
We can make the following table:

Hence option D is correct.
Instructions
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each. Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Question 5: What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?
a) Hi, Lo, Lo, Hi
b) Hi, Lo, Lo, Lo
c) Hi, Hi, Lo, Lo
d) Lo, Lo, Lo, Hi
5) Answer (A)
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:
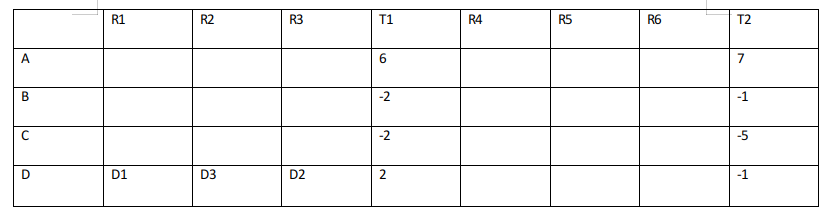
**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)
Hence this case is valid.
The final table looks like:
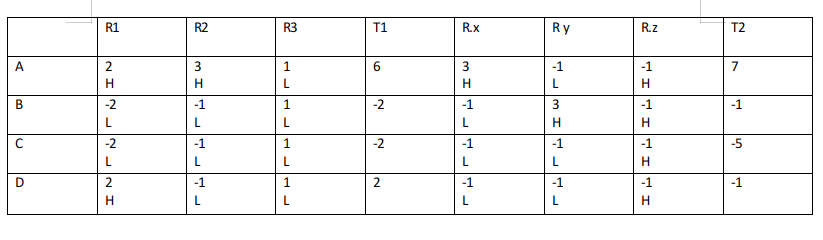
The bids by Arun, Bankim, Charu and Dipak, respectively in the first round are HLLH.
Hence Option A is correct.
Checkout: CAT Free Practice Questions and Videos
Question 6: In how many rounds did Arun bid Hi?
6) Answer: 4
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)
Hence this case is valid.
The final table looks like:

Arun bid high in R1,R2, R.x, R.z hence, 4 is correct answer.
Question 7: In how many rounds did Bankim bid Lo?
7) Answer: 4
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3 so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2 in any possible combination the sum will not be 6. So, this case is invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)
Hence this case is valid.
The final table looks like:

Bikram bid Lo in R1,R2,R3,R.x. Hence 4 is correct answer.
Question 8: In how many rounds did all four players make identical bids?
8) Answer: 2
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)
Hence this case is valid.
The final table looks like:

All the players made identical bids in R3 and R.z
Question 9: In how many rounds did Dipak gain exactly 1 point?
9) Answer: 1
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)
Hence this case is valid.
The final table looks like:

Deepak got exactly one point in only R3.
Hence 1 is correct answer.
Question 10: In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?
a) Second
b) Third
c) Fourth
d) First
10) Answer (A)
Solution:
Let ‘H’ represents Hi and ‘L’ represents Lo.
Given if they bid
Case 1: HHHH then all players gets -1 points.
Case 2: HHHL => H gets +1 and L gets -3.
Case 3: HHLL => H gets +2 and L gets -2.
Case 4: HLLL => H gets +3 and L gets -1.
Case 5: LLLL => every player gets +1.
From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.
**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.
From point 3, D1>D2>D3
D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :
Case D1: 3,2,-3
In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.
Case D2: 2,1,-1
In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.
Case D3: 3,1,-2
In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.
.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.
Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.
Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.
Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.
With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.
Given In exactly two out of the six rounds, Arun was the only player who bid Hi.
Let R.x, R.y, R.z represent R4, R5, R6 in any order.
Let A bid H in R.x=> B,C,D bid L.
The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2
For B, R.x+R.y+R.z=1 => R.y+R.z=2
For C, R.x+R.y+R.z=-3 => R.y+R.z=-2
For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2
(R.y, R.z) for A can be (-3,1) or (-1,-1)
Case A1:
If for A, (R.y, R.z)=(-3,1)
Since for both C,D: R.y+R.z=-2
We can’t get any combination such that the total points of B,C,D are obtained.
Case A2:
If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)
Hence this case is valid.
The final table looks like:

R2 is correct answer.
Instructions
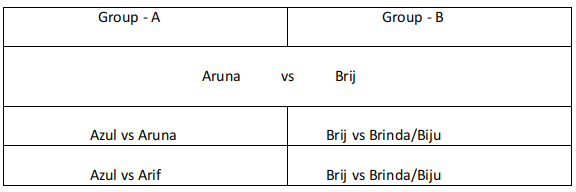
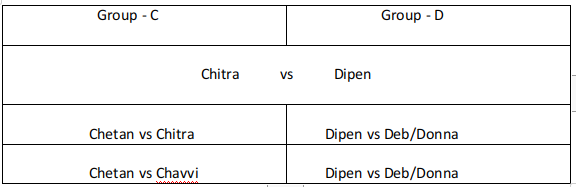
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
1. Chitra did not win the championship.
2. Aruna did not play against Arif. Brij did not play against Brinda.
3. Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
Question 11: Who among the following was DEFINITELY NOT ranked first in his/her group?
a) Dipen
b) Aruna
c) Brij
d) Chitra
11) Answer (A)
Solution:
Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.
Group – C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.
Aruna plays Chitra in the finals and wins the final round.
Dipen was ranked 2 or 3 in his group
Question 12: Which of the following pairs must have played against each other in the championship?
a) Deb, Donna
b) Azul, Biju
c) Donna, Chetan
d) Chitra, Dipen
12) Answer (D)
Solution:
Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.

Group – C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.

Aruna plays Chitra in the finals and wins the final round.
Chitra and Dipen played in the semifinals
Question 13: Who won the championship?
a) Chitra
b) Aruna
c) Brij
d) Cannot be determined
13) Answer (B)
Solution:
Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.

Group – C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.

Aruna plays Chitra in the finals and wins the final round.
Aruna is the winner.
Question 14: Who among the following did NOT play against Chitra in the championship?
a) Aruna
b) Chetan
c) Dipen
d) Biju
14) Answer (D)
Solution:
Group A :
Since Aruna played 3 games if she belongs to rank 2 or rank 3 in her group she must have reached the semifinals and lost in the semifinals. But for this case, she must play against rank 1 and rank 3 in her group. But she did not play against Arif from her group.
Hence Aruna was ranked 1 in her group, Among Azul and Arif one of them was ranked 2 and the other was ranked 3. Azul defeated Arif in the first round and in the second round lost to Aruna. Aruna played her first round with Azul and won the round and played against the winner from group B and defeated them and moved to the finals.
Group B :
Brij did not play against Brinda. Biju played three games, Brij and Brinda played one game each.
Since Brij and Brinda played only one game each one of them was ranked 1 and the other was ranked 2 and 3. Brij did not play against Brinda. We are aware that Aruna reached finals and hence the person from Group B did not reach the finals. Biju played three games and hence must have played with Brij/Brinda in the first round and won the round. Plays with Brij/ Brinda and wins the second round. Plays with Aruna and loses the third round.

Group – C :
Chitra played 2 matches and Chetan played 2 matches. For Chitra to play 2 matches if she is rank 2 or rank 3 in her group. She must at least reach the semifinals. But in this case, Chetan will be defeated in his first round. So Chitra must be ranked 1 in her group and Chetan must be ranked 2 or rank 3 in his group. He defeats Chhavi in his first round and loses to Chitra in his second round. Chitra plays Chetan in her first round, wins over the winner of group D in her second round, and loses in the final against Aruna as per condition 1.
Group -D :
The person from Group D did not reach the finals because Chitra reached the finals. In order for Dipen to play 3 matches before his finals. Dipen must be ranked 2 or rank 3 in his group and plays Deb and Donna in the first two rounds in any order and wins over both of them. Dipen loses to Chitra in his third round.

Aruna plays Chitra in the finals and wins the final round.
Brij was the player from group B who played Chitra. Aruna played in finals, Chetan in round 2, and Dipen in semi finals
Instructions
10 players – P1, P2, … , P10 – competed in an international javelin throw event. The number (after P) of a player reflects his rank at the beginning of the event, with rank 1 going to the topmost player. There were two phases in the event with the first phase consisting of rounds 1, 2, and 3, and the second phase consisting of rounds 4, 5, and 6. A throw is measured in terms of the distance it covers (in meters, up to one decimal point accuracy), only if the throw is a ‘valid’ one. For an invalid throw, the distance is taken as zero. A player’s score at the end of a round is the maximum distance of all his throws up to that round. Players are re-ranked after every round based on their current scores. In case of a tie in scores, the player with a prevailing higher rank retains the higher rank. This ranking determines the order in which the players go for their throws in the next round.
In each of the rounds in the first phase, the players throw in increasing order of their latest rank, i.e. the player ranked 1 at that point throws first, followed by the player ranked 2 at that point and so on. The top six players at the end of the first phase qualify for the second phase. In each of the rounds in the second phase, the players throw in decreasing order of their latest rank i.e. the player ranked 6 at that point throws first, followed by the player ranked 5 at that point and so on. The players ranked 1, 2, and 3 at the end of the sixth round receive gold, silver, and bronze medals respectively.
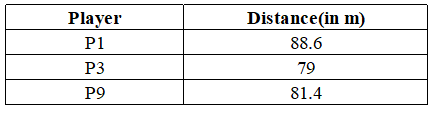
All the valid throws of the event were of distinct distances (as per stated measurement accuracy). The tables below show distances (in meters) covered by all valid throws in the first and the third round in the event.
Distances covered by all the valid throws in the first round

Distances covered by all the valid throws in the third round
The following facts are also known.
i. Among the throws in the second round, only the last two were valid. Both the throws enabled these players to qualify for the second phase, with one of them qualifying with the least score. None of these players won any medal.
ii. If a player throws first in a round AND he was also the last (among the players in the current round) to throw in the previous round, then the player is said to get a double. Two players got a double.
iii. In each round of the second phase, exactly one player improved his score. Each of these improvements was by the same amount.
iv. The gold and bronze medalists improved their scores in the fifth and the sixth rounds respectively. One medal winner improved his score in the fourth round.
v. The difference between the final scores of the gold medalist and the silver medalist, as well as the difference between the final scores of the silver medalist and the bronze medalist was 1.0 m.
Question 15: Which two players got the double?
a) P1, P8
b) P2, P4
c) P8, P10
d) P1, P10
15) Answer (C)
Solution:
Let us arrange the players in the order in which they throw in each round.
Round 1: Here the players throw in order of their initial seeds so the order is as follows:
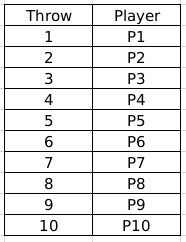
So, their rank at the start of Round 2 is in order of their throws in the first round. Also, we need to consider the same order for people having invalid throws.
Round 2: P2, P4, P8, P10 had the same relative rankings since they all have invalid throws, that is, 0 metres. Rest are arranged as per their throw distances.
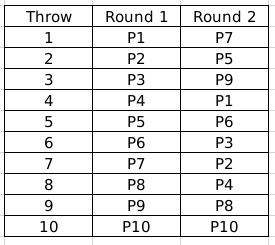
Now, in round 2, only P8 and P10 had valid throws. Hence, their order will change at the start of Round 3, however, the remaining order stays the same. That is, P8 and P10 will move up in the table and occupy some higher places, whereas some of the others may move down consequently.
Round 3: In Round 3, we can see that P1 improved his score from 82.9 to 88.6. The other 2 participants did not improve their scores. Also after Round 3, P8 and P10 qualify, where one of P8 or P10 is at the sixth position. So at the end of Round 3, we can say that P6, P3, P2, and P4 are at the bottom 4 positions(ranks). One of P8 or P10 is at the sixth position. P1 > P7 > P5 > P9.
So at the end of round 3, the ranks are as follows:

The other person between P8/P10 can go anywhere between Rank 1 and Rank 5.
Now let us consider the two players who got a double. Doubles happen in the transition between rounds.
1 -> 2 – Not possible
2 -> 3 – Possible if P10 reaches Rank 1 after round 2.
3 -> 4 – P8/P10 who is the last among qualifying will be the first to throw. So, here it definitely happens.
4 – > 5 AND 5 – > 6 not possible.
So, after Round 2, definitely, P10 reaches the top of the ranking. P8 is at the bottom. Hence, after Round 3, P10 either retains rank 1 or P1 surpasses him and P10 becomes Rank 2.
So, two combinations are possible at the end of Round 3:
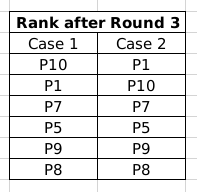
Now, we know that in each of the rounds in phase 2, only one player improves his score. Also, P8 and P10 cannot win medals. Hence, in case 1, three of P1, P7, P5 and P9 will improve their scores by x and reach the top 3 positions. However, the top 3 positions’ distances are in AP.
P1 – 88.6 + x
P7 – 87.2 + x
P5 – 86.4 + x
P9 – 84.1 + x
The differences do not satisfy the condition. Hence, case 1 is invalidated.
Case 2: Here, P1 definitely wins a medal, and P10 does not. So, two of P7, P5 and P9 jumps above P10. Now, if we have three different people increasing their scores or distances in each of the three rounds, again we would not get a difference of 1 among the Gold, Silver and Bronze medallists. Hence, one of them increases his score twice and the other increases his score twice and none of them is P1.
Let us take the cases where P1 is individually the G, S and B medallists.
Case 1: P1 is a G medallist.
P1 – 88.6
The silver medallist is 87.6 and the bronze medallist is 86.6 metres. However, P10 has thrown for a distance that is greater than 87.2 metres. Hence, in this case, he would be the B medallist. Hence, this is not the right case.
Case 2: P1 is the S medallist.
P1 – 88.6
G – 89.6
B – 87.6
Now, if we see the differences
89.6 – 87.2 = 2.4
87.6 – 86.4 = 1.2
This satisfies the condition that P7 has increased his score twice to become the gold winner and P5 has increased it once to become the bronze winner.
Hence, P1 – Silver
P7 – Gold
P5 – Bronze
Hence, P8 and P10 got the doubles.
CAT LRDI Preparation | CAT Preparation Videos
- Try these 3 Cracku Free CAT Mocks, which come with detailed solutions and with video explanations.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
