DILR Questions for CAT PDF (With Solutions)

DILR is one of the most important sections in the CAT Exam. The questions on DILR are usually challenging, and hence students should take this section seriously. It is essential that you know the basics of the CAT DILR well and practice the questions. Also, do check out all the DILR questions for CAT from the CAT Previous Papers with detailed video solutions. This article will look into some important DILR questions for the CAT Exam PDF (with detailed solutions).

As we know, CAT has moved away from the traditional DILR sets, it’s imperative to practice the non-traditional type of sets. The sets that are appearing are more logic-based (and relatively less data-intensive in nature). Hence practice the DILR Sets well; Click on the below link to download the PDF.

Download DILR CAT Questions

Enroll for CAT 2022 Crash Course

Instructions

DIRECTIONS for the following four questions:

A low-cost airline company connects ten India cities, A to J. The table below gives the distance between a pair of airports and the corresponding price charged by the company. Travel is permitted only from a departure airport to an arrival airport. The customers do not travel by a route where they have to stop at more than two intermediate airports.

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_6_3.png”/>

Question 1: What is the lowest possible fare, in rupees, from A to J?

a) 2275

b) 2850

c) 2890

d) 2930

e) 3340

1) Answer (A)

View Video Solution

Solution:

From the table we can see that, the lowest price would be from A to H and H to J.

The cost of travel from A to H = Rs 1850

The cost of travel from H to J = Rs 425

Total cost = 1850 + 425 = Rs 2275.

Question 2: The company plans to introduce a direct flight between A and J. The market research results indicate that all its existing passengers travelling between A and J will use this direct flight if it is priced 5% below the minimum price that they pay at present. What should the company charge approximately, in rupees, for this direct flight?

a) 1991

b) 2161

c) 2707

d) 2745

e) 2783

2) Answer (B)

View Video Solution

Solution:

From the table we can see that, the lowest price would be from A to H and H to J.

The cost of travel from A to H = Rs 1850

The cost of travel from H to J = Rs 425

Total cost = 1850 + 425 = Rs 2275

Lowest price = Rs 2275

95% of 2275 = Rs 2161

Question 3: If the airports C, D and H are closed down owing to security reasons, what would be the minimum price, in rupees, to be paid by a passenger travelling from A to J?

a) 2275

b) 2615

c) 2850

d) 2945

e) 3190

3) Answer (C)

View Video Solution

Solution:

If the airports C, D and H are closed down  the minimum price to be paid by a passenger travelling from A to J would be by first travelling to F and then from F to J.

The cost of travel from A to F = Rs 1700

The cost of travel from F to J = Rs 1150

Total cost = 1700 + 1150 = Rs 2850

Question 4: If the prices include a margin of 10% over the total cost that the company incurs, what is the minimum cost per kilometer that the company incurs in flying from A to J?

a) 0.77

b) 0.88

c) 0.99

d) 1.06

e) 1.08

4) Answer (B)

View Video Solution

Solution:

The minimum cost from A to J we know is 2275.

Let the CP to company be C

Since 10% over actual CP is the total price  i.e.  $\text{CP}\times1.1 = 2275  \rightarrow  CP =  \frac{2275}{1.1}$

The total distance is 1950+1400=2350 Km.

Cost per Km = $\dfrac{\frac{2275}{1.1}}{2350}$ = Rs 0.88/Km

Question 5: If the prices include a margin of 15% over the total cost that the company incurs, which among the following is the distance to be covered in flying from A to J that minimizes the total cost of travel for the company?

a) 2170

b) 2180

c) 2315

d) 2350

e) 2390

5) Answer (D)

View Video Solution

Solution:

Even if If the prices include a margin of 15% over the total cost that the company incurs, the total cost company incurs would be minimum for route AHJ i.e 2350 km. Hence option D.

Checkout: CAT Free Practice Questions and Videos

Instructions

In a certain board examination, students were to appear for examination in five subjects:
English, Hindi, Mathematics, Science and Social Science. Due to a certain emergency situation, a few of the examinations could not be conducted for some students. Hence, some students missed one examination and some others missed two examinations. Nobody missed more than two examinations.

The board adopted the following policy for awarding marks to students. If a student appeared in all five examinations, then the marks awarded in each of the examinations were on the basis of the scores obtained by them in those examinations.

If a student missed only one examination, then the marks awarded in that examination was the average of the best three among the four scores in the examinations they appeared for. If a student missed two examinations, then the marks awarded in each of these examinations was the average of the best two among the three scores in the examinations they appeared for. The marks obtained by six students in the examination are given in the table below. Each of them missed either one or two examinations.

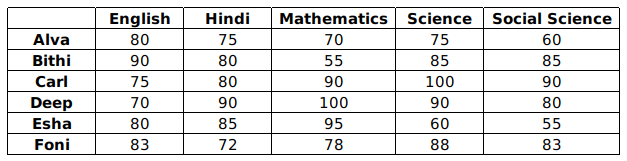
The following facts are also known.
I. Four of these students appeared in each of the English, Hindi, Science, and Social Science examinations.
II. The student who missed the Mathematics examination did not miss any other examination.
III. One of the students who missed the Hindi examination did not miss any other examination. The other student who missed the Hindi examination also missed the Science examination.

Question 6: Who among the following did not appear for the Mathematics examination?

a) Alva

b) Carl

c) Foni

d) Esha

6) Answer (B)

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores.

For Alva: best 3 out of 4 – 80(English), 75(Hindi), 75(Science)

Avg. = 230/3 = 76.67 $\ne\ $ 70

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl most likely missed his Mathematics examination.

For Foni: best 3 out of 4 – 83(English), 83(Social Science), 88(Science)

Avg. = 254/3 = 84.67 $\ne\ $ 78

Hence, we observe that only Carl has missed his Mathematics examination. Hence, Option B is the correct answer.

Question 7: Which students did not appear for the English examination?

a) Carl and Deep

b) Cannot be determined

c) Alva and Bithi

d) Esha and Foni

7) Answer (D)

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl missed his Mathematics examination.

Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.

Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.

For Esha:  best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)

Avg. = 240/3 = 80 which matches the given value

$\therefore\ $ Esha most likely missed her English examination.

For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)

Avg. = 249/3 = 83 which matches the given value

$\therefore\ $ Foni most likely missed her English examination.

Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.

For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.

We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.

For Bithi: Best 2 out 3 – 90(English), 80(Hindi)

Avg = 170/2 = 85 which matches the given value

$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.

We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.

Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).

Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):

Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi

Hence, the correct answer to this question is Option D: Esha and Foni.

Question 8: What BEST can be concluded about the students who did not appear for the Hindi examination?

a) Deep and Esha

b) Alva and Deep

c) Alva and Esha

d) Two among Alva, Deep and Esha

8) Answer (B)

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl missed his Mathematics examination.

Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.

Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.

For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)

Avg. = 240/3 = 80 which matches the given value

$\therefore\ $ Esha most likely missed her English examination.

For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)

Avg. = 249/3 = 83 which matches the given value

$\therefore\ $ Foni most likely missed her English examination.

Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.

For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.

We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.

For Bithi: Best 2 out 3 – 90(English), 80(Hindi)

Avg = 170/2 = 85 which matches the given value

$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.

We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.

Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).

Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):

Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi

Hence, the correct answer to this question is Option B: Alva and Deep.

Question 9: What BEST can be concluded about the students who missed the Science examination?

a) Bithi and one out of Alva and Deep

b) Alva and Bithi

c) Deep and Bithi

d) Alva and Deep

9) Answer (A)

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl missed his Mathematics examination.

Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.

Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.

For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)

Avg. = 240/3 = 80 which matches the given value

$\therefore\ $ Esha most likely missed her English examination.

For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)

Avg. = 249/3 = 83 which matches the given value

$\therefore\ $ Foni most likely missed her English examination.

Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.

For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.

We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.

For Bithi: Best 2 out 3 – 90(English), 80(Hindi)

Avg = 170/2 = 85 which matches the given value

$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.

We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.

Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).

Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):

Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi

Hence, the correct answer to this question is Option A: Bithi & one out of Alva and Deep.

Question 10: How many out of these six students missed exactly one examination?

10) Answer: 3

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl missed his Mathematics examination.

Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.

Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.

For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)

Avg. = 240/3 = 80 which matches the given value

$\therefore\ $ Esha most likely missed her English examination.

For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)

Avg. = 249/3 = 83 which matches the given value

$\therefore\ $ Foni most likely missed her English examination.

Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.

For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.

We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.

For Bithi: Best 2 out 3 – 90(English), 80(Hindi)

Avg = 170/2 = 85 which matches the given value

$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.

We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.

Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).

Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):

Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi

Hence, the correct answer to this question is 3. {Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi)}

Question 11: For how many students can we be definite about which examinations they missed?

11) Answer: 4

View Video Solution

Solution:

Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.

For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)

Avg. = 270/3 = 90 which matches the given value

$\therefore\ $ Carl missed his Mathematics examination.

Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.

Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.

For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)

Avg. = 240/3 = 80 which matches the given value

$\therefore\ $ Esha most likely missed her English examination.

For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)

Avg. = 249/3 = 83 which matches the given value

$\therefore\ $ Foni most likely missed her English examination.

Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.

For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.

We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.

For Bithi: Best 2 out 3 – 90(English), 80(Hindi)

Avg = 170/2 = 85 which matches the given value

$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.

We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.

Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).

Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):

Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi

Except for Alva and Deep, we can conclusively comment of the missed subjects of the rest four. Hence, the correct answer is 4.

Instructions

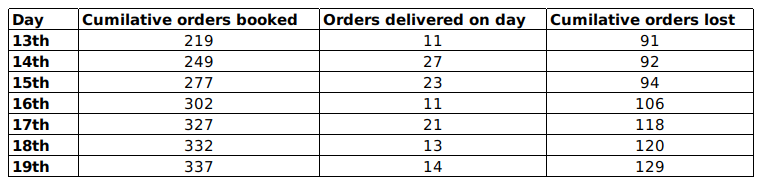
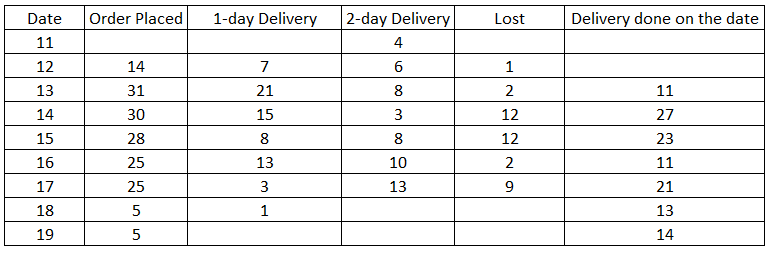
XYZ organization got into the business of delivering groceries to home at the beginning of the last month. They have a two-day delivery promise. However, their deliveries are unreliable. An order booked on a particular day may be delivered the next day or the day after. If the order is not delivered at the end of two days, then the order is declared as lost at the end of the second day. XYZ then does not deliver the order, but informs the customer, marks the order as lost, returns the payment and pays a penalty for non-delivery. The following table provides details about the operations of XYZ for a week of the last month. The first column gives the date, the second gives the cumulative number of orders that were booked up to and including that day. The third column represents the number of orders delivered on that day. The last column gives the cumulative number of orders that were lost up to and including that day. It is known that the numbers of orders that were booked on the 11th, 12th, and 13th of the last month that took two days to deliver were 4, 6, and 8 respectively

Question 12: Among the following days, the largest fraction of orders booked on which day was lost?

a) 15th

b) 16th

c) 13th

d) 14th

12) Answer (A)

View Video Solution

Solution:

The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5

Similarly we can find the orders booked on that day till 14th.

Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1

Similarly, the number of orders lost till 17th can be found out.

Number of orders delivered on 13th are 11 out of which 4 are orders which were booked in 11th so, 7 must be the orders which were booked on 12th.

Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.

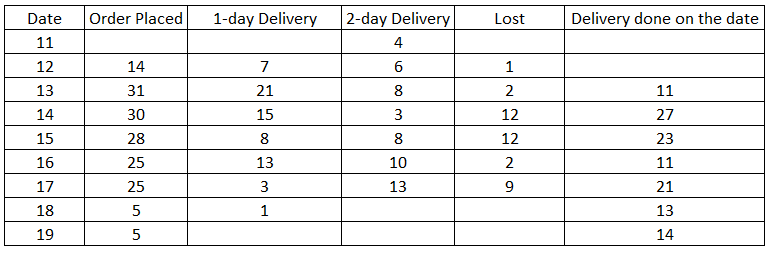
Now, total number of orders booked on 12th will be 7+6=1=14.

Fraction of orders booked on 15th that were lost = 12/28

Fraction of orders booked on 16th that were lost = 2/25

Fraction of orders booked on 13th that were lost =2/31

Fraction of orders booked on 14th that were lost = 8/30.

.’. Option A is correct answer.

Question 13: On which of the following days was the number of orders booked the highest?

a) 12th

b) 15th

c) 13th

d) 14th

13) Answer (C)

View Video Solution

Solution:

The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5

Similarly we can find the orders booked on that day till 14th.

Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1

Similarly, the number of orders lost till 17th can be found out.

Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.

Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.

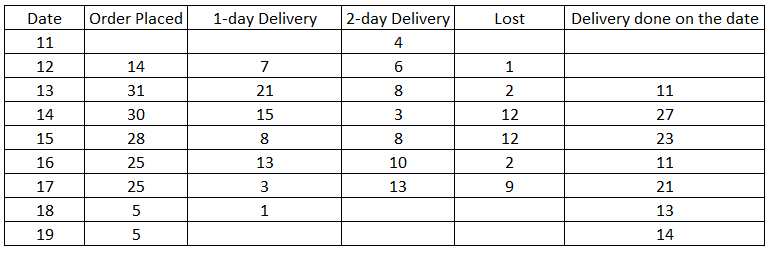
Now, total number of orders booked on 12th will be 7+6+1=14.

The total number of orders placed on 13th = 21+8+2 = 31

FRom the table we can determine that among options, number of orders booked on 13th are maximum.

Question 14: The delivery ratio for a given day is defined as the ratio of the number of orders booked on that day which are delivered on the next day to the number of orders booked on that day which are delivered on the second day after booking. On which of the following days, was the delivery ratio the highest?

a) 15th

b) 16th

c) 13th

d) 14th

14) Answer (D)

View Video Solution

Solution:

The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5

Similarly we can find the orders booked on that day till 14th.

Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1

Similarly, the number of orders lost till 17th can be found out.

Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.

Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.

Now, total number of orders booked on 12th will be 7+6+1=14.

From the table we can determine that among options, number of orders booked on 13th are maximum.

For 15 the delivery ratio = 8/8 = 1

For 16 the delivery ratio = 13/10 = 1.3

For 13 the delivery ratio = 21/8 = 2.625

For 14 the delivery ratio = 15/3 = 5

Hence Option D

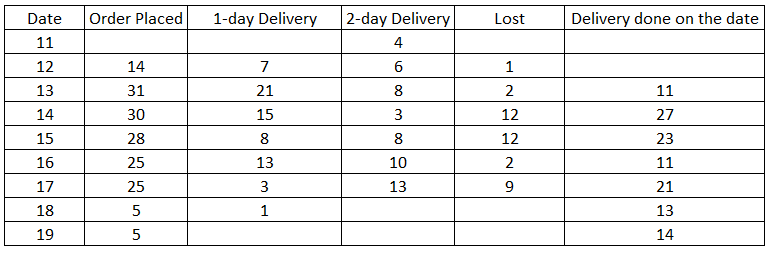
Question 15: The average time taken to deliver orders booked on a particular day is computed as follows. Let the number of orders delivered the next day be x and the number of orders delivered the day after be y. Then the average time to deliver order is $\frac{(x+2y)}{(x+y)}$. On which of the following days was the average time taken to deliver orders booked the least?

a) 15th

b) 13th

c) 14th

d) 16th

15) Answer (C)

View Video Solution

Solution:

The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5

Similarly we can find the orders booked on that day till 14th.

Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1

Similarly, the number of orders lost till 17th can be found out.

Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.

Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.

Now, total number of orders booked on 12th will be 7+6+1=14.

FRom the table we can determine that among options, number of orders booked on 13th are maximum.

Average time can be calculated as follows

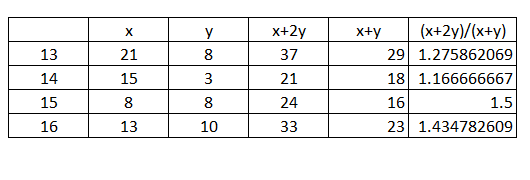
14 is the least

Instructions

Mathematicians are assigned a number called Erdos number (named after the famous mathematician, Paul Erdos). Only Paul Erdos himself has an Erdos number of zero. Any mathematician who has written a research paper with Erdos has an Erdos number of 1.For other mathematicians, the calculation of his/her Erdos number is illustrated below:

Suppose that a mathematician X has co-authored papers with several other mathematicians. ‘From among them, mathematician Y has the smallest Erdos number. Let the Erdos number of Y be y. Then X has an Erdos number of y+1. Hence any mathematician with no co-authorship chain connected to Erdos has an Erdos number of infinity. :

In a seven day long mini-conference organized in memory of Paul Erdos, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdos number. Nobody had an Erdos number less than that of F.

On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdos number of the group of eight mathematicians to 3. The Erdos numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdos number of the group of eight to as low as 3.

• At the end of the third day, five members of this group had identical Erdos numbers while the other three had Erdos numbers distinct from each other.

• On the fifth day, E co-authored a paper with F which reduced the group’s average Erdos number by 0.5. The Erdos numbers of the remaining six were unchanged with the writing of this paper.

• No other paper was written during the conference.

Question 16: The person having the largest Erdos number at the end of the conference must have had Erdos number (at that time):

a) 5

b) 7

c) 9

d) 14

e) 15

16) Answer (B)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20

So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5,one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence the person having the largest Erdos number at the end of the conference must have had Erdos number 7 . Hence option B.

Question 17: How many participants in the conference did not change their Erdos number during the conference?

a) 2

b) 3

c) 4

d) 5

e) Cannot be determined

17) Answer (D)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

So B,D ,F,G,H are 5 participants in the conference who did not change their Erdos number during the conference.

Question 18: The Erdos number of C at the end of the conference was:

a) 1

b) 2

c) 3

d) 4

e) 5

18) Answer (B)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Erdos no. of C at the end is f+1 = 1+1 = 2. Hence option B.

Question 19: The Erdos number of E at the beginning of the conference was:

a) 2

b) 5

c) 6

d) 7

e) 8

19) Answer (C)

View Video Solution

Solution:

Let us consider the Erdos number of A,B,C,D,E,F,G,H be a,b,c,d,e,f,g,h where f is the min, a is infinity.

At the end of 3rd day, F co authored with A and C. Since F has min Erdos number ,the values of c,a will change to f+1 and the Erdos number of F will remain the same.   [Because according to Erdos principle if a person co-authors with some one who has higher Erdos number then the Erdos number of co-authors will be min Erdos value + 1]

Average of the mathematicians is 3
Sum of the Erdos number of eight mathematicians=24

Erdos number at the third day:f+1,b,f+1,d,e,f,g,h

At the end of the fifth day, F co-authors with E thereby changing the average to 2.5 and the Erdos number of rest of the mathematicians remain unchanged.
Sum of the Erdos numbers of eight mathematicians=20
So here the difference of 4[24-20] arose, which means e will be f+5 initially and changed to f+1 after co-authoring with F.

So the Erdos number at the third day:f+1,b,f+1,d,f+5,f,g,h

At the end of the third day, five mathematicians had the same Erdos number and the rest had distinct Erdos number from each other.

It cannot be f+5 because then there will be two mathematicians with the same Erdos number f+1.

So five mathematicians will have f+1, one with f+5, one with f, one with some different value say x

5(f+1)+f+5+f+x=24

7f+x=14

The only value which satisfies the above equation is f=1,x=7

Erdos number at the end of fifth day,f+1,b,f+1,d,f+1,f,g,h
On tabulating, we get

Hence erdos no. of E at the beginning of conference would be f+5 = 6 .

Question 20: How many participants had the same Erdos number at the beginning of the conference?

a) 2

b) 3

c) 4

d) 5

e) Cannot be determined

20) Answer (B)

View Video Solution

Solution:

Since at the end of the 3rd day 5 people had identical erdos no.(f+1) so : 5*(f+1) +f+f+5+x = 24 ; Only f=1 and x = 7 satisfies the equation. So out of 5 people who had identical erdos no. at the end of day 3, 2 of them had different nos. at the beginning. So there were 5-2 = 3 participants who had the same Erdos number at the beginning of the conference.