CAT Coordinate Geometry Questions PDF [Most Important]

Coordinate Geometry is one of the key topics in the CAT Quantitative Ability (QA) section. Usually, the sums in Coordinate Geometry are not tough to solve and hence one must not miss out on the questions on Coordinate Geometry. You can check out these Coordinate Geometry questions from the CAT Previous year’s papers. Practice a good number of questions in CAT Coordinate Geometry so that you can answer these questions with ease in the exam. In this post, we will look into some important Coordinate Geometry Questions for CAT QA. These are a good source for practice; If you want to practice these questions, you can download this Important CAT Coordinate Geometry Questions PDF below, which is completely Free.

Download Coordinate Geometry Questions for CAT

Enroll for CAT 2022 Online Course

Question 1: What is the equation of a circle with centre of origin and radius is 6 cm?

a) $x^2 + y^2 – y = 36$

b) $x^2 + y^2 – x – y = 36$

c) $x^2 + y^2 – 36 = 0$

d) $x^2 + y^2 – x = 36$

1) Answer (C)

Solution:

Given,

Center of the circle = (0,0)

Radius of the circle (r) = 6 cm

$\therefore\ $Equation of the circle is $x^2+y^2=r^2\ $

$=$>  $x^2+y^2=6^2\ $

$=$>  $x^2+y^2=36$

$=$>  $x^2+y^2-36=0$

Hence, the correct answer is Option C

Question 2: The equation of circle with centre (1, -2) and radius 4 cm is:

a) $x^2 + y^2 + 2x – 4y = 11$

b) $x^2 + y^2 + 2x – 4y = 16$

c) $x^2 + y^2 – 2x + 4y = 16$

d) $x^2 + y^2 – 2x + 4y = 11$

2) Answer (D)

Solution:

Given,

Centre of the circle (a, b) = (1, -2)

Radius of the circle (r) = 4 cm

$\therefore\ $Equation of the circle is $\left(x-a\right)^2+\left(y-b\right)^2=r^2$

$=$>  $\left(x-1\right)^2+\left(y-\left(-2\right)\right)^2=4^2$

$=$>  $\left(x-1\right)^2+\left(y+2\right)^2=4^2$

$=$>  $x^2+1^2-2.x.1+y^2+2^2+2.y.2=16$

$=$>  $x^2+1-2x+y^2+4+4y=16$

$=$>  $x^2-2x+y^2+4y=16-1-4$

$=$>  $x^2+y^2-2x+4y=11$

Hence, the correct answer is Option D

Question 3: In $\triangle ABC, AB = AC$. A circle drawn through B touches AC at D and intersect AB at P. If D is the mid point of AC and AP 2.5 cm, then AB is equal to:

a) 9 cm

b) 10 cm

c) 7.5 cm

d) 12.5 cm

3) Answer (B)

Solution:

Given D is midpoint of AC so,

AD = $\frac{AC}{2}$

But also given AC = AB

AD = $\frac{AB}{2}$ —-(1)

AD is a tangent and APB is a secant. So the tangent secant theorem can be applied,

$AD^2 = AP \times AB$

$(\frac{AB}{2})^2 = 2.5 \times AB$

$\frac{AB^2}{4} = 2.5 \times AB$

AB = 10 cm

Question 4: The graph of the equations $5x – 2y + 1 = 0$ and $4y – 3x + 5 = 0$, interest at the point $P(\alpha, \beta)$, What is the value of $(2\alpha – 3\beta)$?

a) 4

b) 6

c) -4

d) -3

4) Answer (A)

Solution:

$5x – 2y + 1 = 0$
15x – 6y + 3 = 0 —(1)
$3x -4y – 5 = 0$
15x – 20y – 25 = 0 —(2)
From eq (1) and (2),
14y + 28 = 0
y = -2
From eq(1),
15x + 6$\times 2$ + 3 = 0
x = -1
$\alpha$ = -1
$\beta$ = -2
$(2\alpha – 3\beta)$
= $(2 \times (-1) + 3\times 2)$ = 4

Question 5: What is the area (in square units) of the triangular region enclosed by the graphs of the equations x + y = 3, 2x + 5y = 12 and the x-axis?

a) 2

b) 3

c) 4

d) 6

5) Answer (B)

Solution:

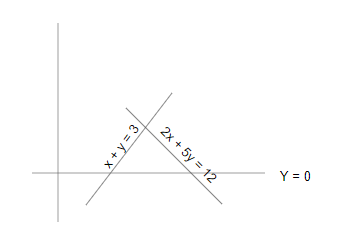
x + y = 3
2x + 2y = 6 —(1)
2x + 5y = 12 —(2)
From eq (1) and eq (2),
3y = 6
y = 2
So height = 2
y = 0 —(3)
put the value of y in eq(1) and (2),
2x = 6
x = 3
And 2x = 12
x = 6
Area = $\frac{1}{2} \times base \times height$
= $\frac{1}{2} \times (6 – 3) \times 2$ = 3 square units

Checkout: CAT Free Practice Questions and Videos

Question 6: The graphs of the equations $2x + 3y = 11$ and $x – 2y + 12 = 0$ intersects at $P(x_1, y_1)$ and the graph of the equations $x – 2y + 12 = 0$ intersects the x-axis at $Q (x_2, y_2)$. What is the value of $(x_1 – x_2 + y_1 + y_2)$?

a) 13

b) -11

c) 15

d) -9

6) Answer (C)

Solution:

$2x + 3y = 11$ —(1)
$x – 2y + 12 = 0$
$2x – 4y = -24$ —(2)
From eq (1) and (2),
7y = 35
y = 5 = $y_1$
From eq (1),
$2x + 3 $\times$ 5 = 11$
2x = -4
x = -2 = $x_1$
Now,
The graph of the equations $x – 2y + 12 = 0$ intersects the x-axis.
So,
$ y = y_1$ = 0
$x – 0 + 12 = 0$
x = -12 = $x_1$
$(x_1 – x_2 + y_1 + y_2)$
= -2 + 12 + 5 + 0 = 15

Question 7: The point of intersection of the graphs of the equations 3x — 5y = 19 and 3y —7x + 1 =0 is P$\left(\alpha,\beta\right)$ . Whatis the value of $ \left(3\alpha -\beta \right)$ ?

a) -2

b) -1

c) 1

d) 0

7) Answer (B)

Solution:

The point of intersection of the graphs of the equations 3x — 5y = 19 and 3y —7x + 1 =0 is P$\left(\alpha,\beta\right)$
So,
3$\alpha — 5\beta = 19$ —(1)
7$\alpha — 3\beta = 1$ —(2)
Eq(1) multiply by 3 and eq (2) multiply by 5,
9$\alpha — 15\beta = 57$ —(1)
35$\alpha — 15\beta = 5$ —(2)
From eq (3) and (4),
26$\alpha = -52$
$\alpha = -2$
From eq (1),
3$\times -2 – 5\beta = 19$
$\beta = -5$
Now,
$ \left(3\alpha -\beta \right)$
= $ \left(3\times -2 + 5s \right)$
= -1

Question 8: The graph of the equation x — 7y = —42, intersects the y-axis at $P\left(\alpha,\beta\right)$ and the graph of 6x + y – 15 = 0, intersects the x-axis at $Q\left(\gamma,\delta\right)$, What is the value of $\alpha+\beta+\gamma+\delta?$

a) $\frac{17}{2}$

b) 6

c) $\frac{9}{2}$

d) 5

8) Answer (A)

Solution:

The graph of the equation x — 7y = —42, intersects the y-axis at $P\left(\alpha,\beta\right)$
So, x = 0
0 – 7y = -42
y = 6
$\alpha$ = 0
$\beta$ = 6
graph of 6x + y – 15 = 0, intersects the x-axis at $Q\left(\gamma,\delta\right)$
So, y = 0
6x – 15 = 0
x = 5/2
$\gamma$ = 5/2
$\delta$ = 0
Now,
$\alpha+\beta+\gamma+\delta$
= 0 + 6 + 5/2 + 0 = $\frac{17}{2}$

Question 9: The graphs of the equations $3x + y – 5 = 0$ and $2x – y – 5 = 0$ intersect at the point $P(\alpha, \beta)$. What is the value of $(3\alpha + \beta)$?

a) 4

b) -4

c) 3

d) 5

9) Answer (D)

Solution:

When  graphs of the equations intersect at the point $P(\alpha, \beta)$ then,
$3\alpha + \beta – 5 = 0$ —(1)
$2\alpha – \beta – 5 = 0$ —(2),
On eq(1) + (2),
$5\alpha – 10 = 0$
$\alpha = 2$
From the eq(2),
$3 \times 2+ \beta – 5 = 0$
$\beta = -1$
Now,
$(3\alpha + \beta)$ = 3 $\times$ 2 – 1 = 6 – 1 = 5
$\therefore$ The correct answer is option D.

Question 10: The graph of x + 2y = 3 and 3x – 2y = 1 meet the Y-axis at two points having distance

a) $\frac{8}{3}$ units

b) $\frac{4}{3}$ units

c) 1 units

d) 2 units

10) Answer (D)

Solution:

on Y axis, x=0

put x = 0 in x+2y = 3

2y = 3

$ y = \frac{3}{2} $

putting x=0 in 3x-2y = 1

-2y = 1

$ \frac{-1}{2} $

therefore points on Y-axis are

$ (0,\frac{3}{2}) and (0,\frac{-1}{2}) $

required distance = $ \sqrt ((0-0)^2 + \sqrt (\frac{3}{2} + \frac{1}{2})^2 $

$ = \sqrt (0+4) $ = 2 units

Question 11: ABCDis a cyclic quadrilateral, AB and DC when produced meet at P, if PA = 8 cm, PB = 6 cm, PC = 4 cm, then the length (in cm) of PDis

a) 6

b) 12

c) 8

d) 10

11) Answer (B)

Solution:

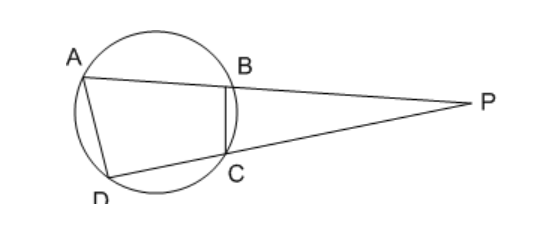
Given that,PA = 8 cm, PB = 6 cm, PC = 4 cm

As per tangent & secant rule,

$ PA \times PB = PD \times PC $

=>$ PD = \frac{8\times6}{4}=12cm $

Question 12: In a circle, chords AD and BC meet at a point E outside the circle. If $\angle$BAE = 76$^\circ$ and $\angle$ADC= 102$^\circ$ , then $\angle$AEC is equal to:

a) $25^\circ$

b) $28^\circ$

c) $26^\circ$

d) $24^\circ$

12) Answer (C)

Solution:

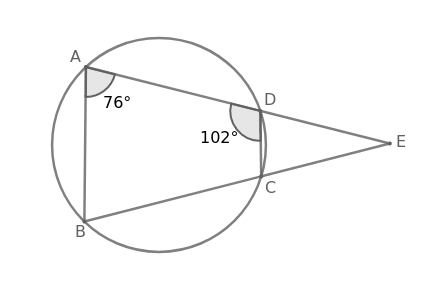
In cyclic quadrilateral ABCD, sum of opposite angles = 180$^\circ$

$=$>  $\angle$BAE + $\angle$BCD = 180$^\circ$

$=$>   76$^\circ$ + $\angle$BCD = 180$^\circ$

$=$>   $\angle$BCD = 104$^\circ$

From the figure,

$\angle$ADC + $\angle$EDC = 180$^\circ$

$=$>  102$^\circ$ + $\angle$EDC = 180$^\circ$

$=$>  $\angle$EDC = 78$^\circ$

$\angle$BCD + $\angle$ECD = 180$^\circ$

$=$> 104$^\circ$ + $\angle$ECD = 180$^\circ$

$=$> $\angle$ECD = 76$^\circ$

In $\triangle\ $CDE,

$\angle$DEC + $\angle$ECD + $\angle$EDC = 180$^\circ$

$=$>  $\angle$AEC + 76$^\circ$ + 78$^\circ$ = 180$^\circ$

$=$>  $\angle$AEC + 154$^\circ$ = 180$^\circ$

$=$>  $\angle$AEC = 26$^\circ$

Hence, the correct answer is Option C

Question 13: If $ \triangle$ABC, $\angle$ABC=90$^\circ$ and BD$\bot$AC , if AD = 4cm and CD = 5cm then BD is equal to

a) $3\sqrt{5}$

b) $2\sqrt{5}$

c) $3\sqrt{2}$

d) $4\sqrt{5}$

13) Answer (B)

Solution:

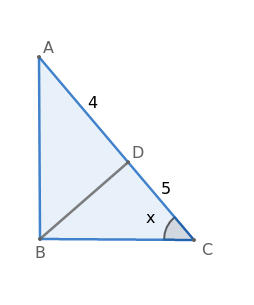
Let $\angle\ $C = x

In $ \triangle$ABC,

$\cos x$ = $\frac{BC}{9}$

$=$>  BC = 9 $\cos x$

In $ \triangle$BCD,

$\cos x$ = $\frac{5}{BC}$

$=$>  $\cos x=\frac{5}{9\cos x}$

$=$>  $\cos^2x=\frac{5}{9}$

$=$>  $\cos x=\frac{\sqrt{5}}{3}$

$=$>  $\sin x=\sqrt{1-\cos^2x}=\sqrt{1-\frac{5}{9}}=\sqrt{\frac{4}{9}}=\frac{2}{3}$

In $ \triangle$BCD,

$\sin x=\frac{BD}{BC}$

$=$>  $\frac{2}{3}=\frac{BD}{9\cos x}$

$=$>  $\frac{2}{3}=\frac{BD}{9\left(\frac{\sqrt{5}}{3}\right)}$

$=$>  $\frac{2}{3}=\frac{3BD}{9\left(\sqrt{5}\right)}$

$=$>  BD = 2$\sqrt{5}$

Hence, the correct answer is Option B

Question 14: In $\triangle$ABC, $\angle$ A= 72$^\circ$. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the $\angle$CBD and $\angle$BCE meet at point O, then $\angle$BOC is equal to:

a) $16^\circ$

b) $54^\circ$

c) $32^\circ$

d) $106^\circ$

14) Answer (B)

Solution:

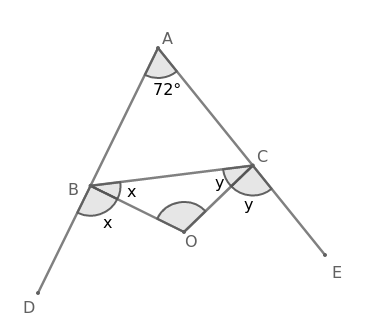
Given,

In $\triangle$ABC, $\angle$A = 72$^\circ$

OB is the angular bisector of $\angle$CBD

$=$> $\angle$OBD = $\angle$OBC

Let $\angle$OBD = $\angle$OBC = $x$

OC is the angular bisector of $\angle$BCE

$=$> $\angle$OCE = $\angle$OCB

Let $\angle$OCE = $\angle$OCB = $y$

From the figure,

$\angle$ABC + $\angle$CBD = 180$^\circ$

$=$> $\angle$ABC + $x$ + $x$ = 180$^\circ$

$=$> $\angle$ABC = 180$^\circ$- 2$x$

$\angle$ACB + $\angle$BCE = 180$^\circ$

$=$> $\angle$ACB + $y$ + $y$ = 180$^\circ$

$=$> $\angle$ACB = 180$^\circ$- 2$y$

In $\triangle$ABC,

$\angle$ABC + $\angle$ACB + $\angle$BAC = 180$^\circ$

$=$> 180$^\circ$- 2$x$ + 180$^\circ$- 2$y$ + 72$^\circ$ = 180$^\circ$

$=$> 2$x$ + 2$y$ = 180$^\circ$ + 72$^\circ$

$=$> 2$(x+y)$ = 252$^\circ$

$=$> $x+y$ = 126$^\circ$ ………………..(1)

In $\triangle$OBC,

$\angle$OBC + $\angle$OCB + $\angle$BOC = 180$^\circ$

$=$> $x$ + $y$ + $\angle$BOC = 180$^\circ$

$=$> 126$^\circ$ + $\angle$BOC = 180$^\circ$

$=$> $\angle$BOC = 180$^\circ$- 126$^\circ$

$=$> $\angle$BOC = 54$^\circ$

Hence, the correct answer is Option B

Question 15: The distance between the centres of two circles of radius 2.5 cm each is 13 cm. The length (in cm)of a transverse common tangent is:

a) 12

b) 8

c) 6

d) 10

15) Answer (A)

Solution:

Radius of first circle ($r_1$) = 2.5 cm

Radius of second circle ($r_2$) = 2.5 cm

The distance between centres of two circles ($d$) = 13 cm

$\therefore\ $Length of the common tangent = $\sqrt{d^2-\left(r_1+r_2\right)^2}$

$=\sqrt{13^2-\left(2.5+2.5\right)^2}$

$=\sqrt{169-25}$

$=\sqrt{144}$

$=$ 12 cm

Hence, the correct answer is Option A

Question 16: ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and $\angle$ADC = 126$^\circ$. $\angle$BAC is equal to:

a) $24^\circ$

b) $72^\circ$

c) $18^\circ$

d) $36^\circ$

16) Answer (D)

Solution:

In cyclic quadrilateral ABCD, sum of opposite angles = 180$^\circ$

$=$>  $\angle$ADC + $\angle$ABC = 180$^\circ$

$=$>   126$^\circ$ + $\angle$ABC = 180$^\circ$

$=$>   $\angle$ABC = 54$^\circ$

Angle subtended by diameter in a semicircle is 90$^\circ$

$=$>  $\angle$ACB = 90$^\circ$

In $\triangle\ $ACB,

$\angle$BAC + $\angle$ACB + $\angle$ABC = 180$^\circ$

$=$>  $\angle$BAC + 90$^\circ$ + 54$^\circ$ = 180$^\circ$

$=$>  $\angle$BAC + 144$^\circ$ = 180$^\circ$

$=$>  $\angle$BAC = 36$^\circ$

Hence, the correct answer is Option D

Question 17: In $\triangle$ABC, $\angle$A = 52$^\circ$. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the $\angle$CBD and $\angle$BCE meet at point O, then $\angle$BOC is equal to:

a) $64^\circ$

b) $16^\circ$

c) $106^\circ$

d) $32^\circ$

17) Answer (A)

Solution:

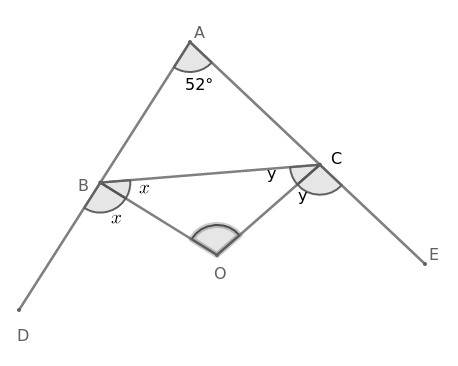
Given,

In $\triangle$ABC,  $\angle$A = 52$^\circ$

OB is the angular bisector of $\angle$CBD

$=$>  $\angle$OBD = $\angle$OBC

Let $\angle$OBD = $\angle$OBC = $x$

OC is the angular bisector of $\angle$BCE

$=$>  $\angle$OCE = $\angle$OCB

Let $\angle$OCE = $\angle$OCB = $y$

From the figure,

$\angle$ABC + $\angle$CBD = 180$^\circ$

$=$>  $\angle$ABC + $x$ + $x$ = 180$^\circ$

$=$> $\angle$ABC  = 180$^\circ$- 2$x$

$\angle$ACB + $\angle$BCE = 180$^\circ$

$=$> $\angle$ACB + $y$ + $y$ = 180$^\circ$

$=$> $\angle$ACB = 180$^\circ$- 2$y$

In $\triangle$ABC,

$\angle$ABC + $\angle$ACB + $\angle$BAC = 180$^\circ$

$=$>  180$^\circ$- 2$x$ + 180$^\circ$- 2$y$ + 52$^\circ$ = 180$^\circ$

$=$>  2$x$ + 2$y$ = 180$^\circ$ + 52$^\circ$

$=$>  2$(x+y)$ = 232$^\circ$

$=$>  $x+y$ = 116$^\circ$ ………………..(1)

In $\triangle$OBC,

$\angle$OBC + $\angle$OCB + $\angle$BOC = 180$^\circ$

$=$>  $x$ + $y$ + $\angle$BOC = 180$^\circ$

$=$>  116$^\circ$ + $\angle$BOC = 180$^\circ$

$=$>  $\angle$BOC = 180$^\circ$- 116$^\circ$

$=$>  $\angle$BOC = 64$^\circ$

Hence, the correct answer is Option A

Question 18: PA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If $\angle$APB = 72$^\circ$, then $\angle$OAB is equal to:

a) $24^\circ$

b) $18^\circ$

c) $36^\circ$

d) $72^\circ$

18) Answer (C)

Solution:

Given,  $\angle$APB = 72$^\circ$

PA and PB are the tangents to the circle with centre O

$=$>  $\angle$OAP = 90$^\circ$ and  $\angle$OBP = 90$^\circ$

In quadrilateral OAPB,

$\angle$AOB + $\angle$OBP + $\angle$APB + $\angle$OAP = 360$^\circ$

$=$>  $\angle$AOB + 90$^\circ$ + 72$^\circ$ + 90$^\circ$ = 360$^\circ$

$=$>  $\angle$AOB + 252$^\circ$ = 360$^\circ$

$=$>  $\angle$AOB = 108$^\circ$

In $\triangle\ $OAB, OA = OB

Angles opposite to equal sides are equal in triangle

$=$>  $\angle$OBA = $\angle$OAB

In $\triangle\ $OAB,

$\angle$AOB + $\angle$OBA + $\angle$OAB = 180$^\circ$

$=$>  108$^\circ$ + $\angle$OAB + $\angle$OAB = 180$^\circ$

$=$>   2$\angle$OAB = 72$^\circ$

$=$>   $\angle$OAB = 36$^\circ$

Hence, the correct answer is Option C

Question 19: The distance between the centres of two circles of radius 3 cm and 2 cm is 13 cm. The length (in cm) of a transverse common tangent is:

a) 8

b) 12

c) 6

d) 10

19) Answer (B)

Solution:

Radius of first circle ($r_1$) = 3 cm

Radius of second circle ($r_2$) = 2 cm

The distance between centres of two circles ($d$) = 13 cm

$\therefore\ $Length of the common tangent = $\sqrt{d^2-\left(r_1+r_2\right)^2}$

$=\sqrt{13^2-\left(3+2\right)^2}$

$=\sqrt{169-25}$

$=\sqrt{144}$

$=$ 12 cm

Hence, the correct answer is Option B

Question 20: The distance between the centre of two circles of radius 4 cm and 2 cm is 10 cm. The length (in cm) of a transverse common tangent is:

a) 4

b) 6

c) 10

d) 8

20) Answer (D)

Solution:

Given, distance between centres of circles$(d)$ = 10 cm

Radius of first circle$(r_1)$ = 4 cm

Radius of second circle$(r_2)$ = 2 cm

$\therefore\ $The length of tranverse common tangent
= $\sqrt{d^2-\left(r_1+r_2\right)^2}=\sqrt{10^2-\left(4+2\right)^2}=\sqrt{100-36}=8\ cm$

Question 21: Chords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is:

a) 5

b) 7

c) 6

d) 2

21) Answer (A)

Solution:

Given,

AB = 6 cm, CD = 3 cm and PB = 4 cm

Let PD = $x$ cm

If chords AB and CD of a circle intersect externally at P then $\text{PA}\times \text{PB}=\text{PC}\times \text{PD}$

$=$>  $\left(AB+PB\right)\times PB=\left(CD+PD\right)\times PD$

$=$>  $\left(6+4\right)\times4=\left(3+x\right)\times x$

$=$>  $40=3x+x^2$

$=$>  $x^2+3x-40=0$

$=$>  $x^2+8x-5x-40=0$

$=$>  $x\left(x+8\right)-5\left(x+8\right)=0$

$=$>  $\left(x+8\right)\left(x-5\right)=0$

$=$>  $x+8=0$  or   $x-5=0$

$=$>  $x=-8$   or  $x=5$

$x$ cannot be negative

$=$>  $x=5$

$\therefore\ $PD = $x$ = 5 cm

Hence, the correct answer is Option A

Question 22: There are two circles of radius 5 cm and 3 cm respectively. The distance between their centres is 10 cm. The length (in cm) of a transverse common tangent is:

a) 9

b) 8

c) 10

d) 6

22) Answer (D)

Solution:

Given, distance between centres of circles$(d)$ = 10 cm

Radius of first circle$(r_1)$ = 5 cm

Radius of second circle$(r_2)$ = 3 cm

$\therefore\ $The length of tranverse common tangent = $\sqrt{d^2-\left(r_1+r_2\right)^2}=\sqrt{10^2-\left(5+3\right)^2}=\sqrt{100-64}=6\ cm$

Question 23: The chord of the contact of tangents drawn from point on the circle $x^2 + y^2 = a^2$ to the circle $x^2 + y^2 = b^2$ touches the circle $x^2 + y^2 = c^2$ such that $b^p = a^m c^n$ where $m, n, p \in N$, and m, n, p are prime to each other, then the value of 2m + n + 2p – 3 is:

a) 5

b) 4

c) 6

d) 2

23) Answer (B)

Solution:

The chord of the contact of tangents drawn from point on the circle $x^2 + y^2 = a^2$ to the circle $x^2 + y^2 = b^2$ touches the circle $x^2 + y^2 = c^2$ then  $a$, $b$, $c$ are in G.P

$=$>   $b^2=ac$ ………………..(1)

Given,  $b^p = a^m c^n$ ………..(2)

Comparing equation (1) and equation (2)

p = 2, m = 1, n = 1

$\therefore\ $2m + n + 2p – 3 = 2(1) + 1 + 2(2) – 3 = 2 + 1 + 4 -3 = 4

Hence, the correct answer is Option B

Question 24: O is the centre of a circle to which PAX and PBY are tangents from point P at points A and B.Q is a point on the circle, such that $\angle$QAX = $49^\circ$ and $\angle$QBY = $62^\circ$. What is the measure of $\angle$AQB ?

a) $63^\circ$

b) $67^\circ$

c) $59^\circ$

d) $69^\circ$

24) Answer (D)

Solution:

Given,
$\angle$QAX = $49^\circ$
$\angle$QBY = $62^\circ$
PAX and PBY are tangents at A and B respectively to the circle
$=$> $\angle$OAX = $90^\circ$ and $\angle$OBY = $90^\circ$
$\angle$OAX = $90^\circ$
$=$> $\angle$QAX + $\angle$QAO = $90^\circ$
$=$> $49^\circ$ + $\angle$QAO = $90^\circ$
$=$> $\angle$QAO = $41^\circ$
$\angle$OBY = $90^\circ$
$=$> $\angle$QBY + $\angle$QBO = $90^\circ$
$=$> $62^\circ$ + $\angle$QBO = $90^\circ$
$=$> $\angle$QAO = $28^\circ$
Angles opposite to equal sides in a triangle are equal
OA = OQ
$=$> $\angle$AQO = $41^\circ$
OB = OQ
$=$> $\angle$BQO = $28^\circ$
$\therefore\ $ $\angle$AQB = $\angle$AQO + $\angle$BQO = $41^\circ$ + $28^\circ$ = $69^\circ$
Hence, the correct answer is Option D

Question 25: In $\triangle$ABC, BD $\perp$ AC. E is point on BC such that $\angle$BEA = $x^\circ$. If $\angle$EAC = $38^\circ$ and $\angle$EBD = $40^\circ$, then the value of x is:

a) $78^\circ$

b) $68^\circ$

c) $72^\circ$

d) $88^\circ$

25) Answer (D)

Solution:

BD $\perp$ AC

$=$> $\angle$BDC = $90^\circ$

In $\triangle\ $BDC,

$\angle$DBC +$\angle$BDC + $\angle$BCD = $180^{\circ\ }$

$=$>  $40^{\circ\ }+90^{\circ\ }$+ $\angle$BCD=$180^{\circ\ }$

$=$>  $\angle$BCD = $50^{\circ\ }$

In $\triangle\ $AEC

$\angle$AEB is the exterior angle at E is equal to the sum of the interior angle at A and C

$=$> $\angle$AEB = $\angle$EAC + $\angle$ACE

$=$> $x^{\circ\ }=38^{\circ\ }+50^{\circ\ }$

$=$> $x^{\circ\ }=88^{\circ\ }\ $

Hence, the correct answer is Option D