Quadrilateral Geometry Questions for SSC MTS

Here you can download the Quadrilateral Geometry Questions for SSC MTS PDF with solutions by Cracku. These are the most important Quadrilateral Geometry questions PDF prepared by various sources also based on previous year’s papers. Utilize this PDF for Quadrilateral Geometry for SSC MTS preparation. You can find a list of the most important Quadrilateral Geometry questions in this PDF, which will help you to test yourself and practice. So you can click on the below link to download the PDF for reference and do more practice.

Download Quadrilateral Geometry Questions for SSC MTS

Enroll to 15 SSC MTS 2022 Mocks At Just Rs. 149

Question 1: Among the following options, the CORRECT one is
1. Rhombus is a cyclic quadrilateral
2. Diagonals of a rhombus are equal
3. A rhombus that can be inscribed in a circle is a square
4. Opposite angles in a rhombus are equal

a) Both 1 and 2

b) Both 1 and 4

c) Both 1 and 3

d) Both 3 and 4

1) Answer (D)

Solution:

Rhombus is not a cyclic quadrilateral as the sum of opposite angles is not always 180 degrees.

Diagonals of a rhombus are not equal except in the case of a square.

A rhombus which is inscribed in a circle is always a square as it will be a cyclic quadrilateral for which the sum of opposite angles must be 180 degrees which is possible only when it is a square.

The opposite angles of a rhombus are equal.

Question 2: In the adjoining figure, ABCD is a cyclic quadrilateral. If AB is a diameter, BC = CD and $\angle ABD = 40^\circ$, find the measure of $\angle DBC$.

a) 65

b) 25

c) 45

d) 60

2) Answer (B)

Solution:

Since AB is the diameter $\angle\ ADB\ =\ 90^0$

Which gives $\angle\ DAB\ =\ 50^0$

ABCD is cyclic quadrilateral so $\angle\ A+\angle\ C\ =\ 180^0$

Thus $\angle\ DCB\ =\ 130^0$

In$\bigtriangleup\ $ BCD, 2x+130 = 150

$x\ =\ 25^0$

Question 3: In the quadrilateral $ABCD$ below, $\angle DAB$ = 90° and $AB = 24$cm , $BC = 40$cm, $CD = 50$cm and $AD = 18$cm(The diagram is not drawn to scale) Find the area of the quadrilateral

a) 1089 $cm^2$

b) 914 $cm^2$

c) 816 $cm^2$

d) 726 $cm^2$

3) Answer (C)

Solution:

Join BD

Area of ABCD = area of ABD + area of BCD

In ABD $AB^2\ +\ AD^2\ =BD^2$

Therefore   $24^{2\ }+\ 18^{2\ }=\ BD^2$ , on solving BD= 30

also $30^{2\ }+\ 40^2\ =50^2$ which implies BCD is also a right-angled triangle

Area of ABD = $\frac{1}{2}\times\ 24\times\ 18$ = 216

Area of BCD = $\frac{1}{2}\times\ 30\times\ 40$= 600

Area of ABCD = 816

Question 4: Let PQRS be a cycle quadrilateral. Let O be the centre of the circumcircle of the quadrilateral. Then which of the following statements is NOT true?

a) $\angle PRQ = \angle POQ$

b) $\angle POQ = 2\angle PSQ$

c) $\angle OPS = \angle OSP$

d) $\angle PRQ = \angle PSQ$

4) Answer (A)

Solution:

The angle which an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

$\angle\ POQ=2\angle\ PSQ$

Angles in the same segment of a circle are equal to one another

$\angle\ PRQ=\angle\ PSQ$

OPS is isosceles ( OP =OS =radius)

$\angle\ OPS=\angle\ OSP$

$\angle\ PRQ\ \ne\ \angle\ POQ$

Question 5: ABCD is a quadrilateral inscribed in a circle with centre O such that O lies inside the quadrilateral. If $\angle COD = 120$ degrees and $\angle BAC = 30$ degrees, then the value of $\angle BCD$ (in degrees) is

5) Answer: 90

View Video Solution

Solution:

$\angle COD = 120$ => $\angle CAD = 120/2 = 60$ (The angle subtended by the chord DC at the major arc is half the angle subtended at the centre of the circle.)
$\angle BAC = 30$
$\angle BAD = \angle BAC + \angle CAD$ = 30 + 60 = 90.
$\angle BCD = 180 – \angle BAD$ = 180 – 90 = 90

Take a free SSC MTS Tier-1 mock test

Download SSC CGL Tier-1 Previous Papers PDF

Question 6: AB, CD and EF are three parallel lines, in that order. Let d1 and d2 be the distances from CD to AB and EF respectively. d1 and d2 are integers, where d1 : d2 = 2 : 1. P is a point on AB, Q and S are points on CD and R is a point on EF. If the area of the quadrilateral PQRS is 30 square units, what is the value of QR when value of SR is the least?

a) slightly less than 10 units

b) 10 units

c) slightly greater than 10 units

d) slightly less than 20 units

e) slightly greater than 20 units

6) Answer (E)

Solution:

There are 3 parallel lines AB, CD, and EF, in that order.
Let the distance between CD and AB be 2x.
It has been given that the distance between CD and EF is x.

A quadrilateral PQRS is formed such that P is on AB, Q and S are on CD, and R is on EF.
Also, the length of SR is the least possible value it can take. Therefore, SR must be perpendicular to the parallel lines.

Area of quadrilateral PQRS = Area of triangle PQS + Area of triangle SRQ = 30 square cm.

Area of triangle PQS = 2*area of triangle SRQ (Since they rest on the same base and height of SRQ is half the height of PQS)
=> Area of triangle SRQ = 10 square cm.
Let the length of SQ be $b$. We know that SR= $x$
$0.5*x*s = 10$
=> $xs=20$
$s=20/x$
We do not have any other detail to evaluate the value of the expression. But, we have been given that d1 and d2 are integers. Therefore, the least value that ‘x’ can take is 1.
The least value that S can take is 1.
By Pythagoras theorem, $QR =\sqrt{s^2 + x^2}$
$QR=\sqrt{20^2+1}$
$QR=\sqrt{401}$
Therefore, the value of QR will be slightly greater than 20. Therefore, option E is the right answer.

Question 7: Eight points lie on the circumference of a circle. The difference between the number of triangles and the number of quadrilaterals that can be formed by connecting these points is

a) 7

b) 14

c) 32

d) 84

7) Answer (B)

Solution:

The number of quadrilaterals that can be made using any 4 points out of total 8 points on the given circle = $^8C_4$ = 70
The number of triangle that can be made using any 4 points out of total 8 points on the given circle = $^8C_3$ = 56
Thus, the required difference = 70-56 = 14
Hence, option B is the correct answer.

Question 8: If there is threefold increase in all the sides of a cyclic quadrilateral, then the percentage increase in its area will be:

a) 81%

b) 9%

c) 900%

d) None of the above

8) Answer (D)

Solution:

Let $a, b, c$ and $d$ be the sides of the cyclic quadrilateral.
Thus, $s = \frac{(a+b+c+d)}{2}$
$Area = \sqrt{(s-a)(s-b)(s-c)(s-d)}$
Thus, after a threefold increase in the sides the sides will become $4a, 4b, 4c$ and $4d$.
Thus new $s = s_{new} = (4a+4b+4c+4d)/2 = 4s$
Thus, $Area_{new} = \sqrt{(4s-4a)(4s-4b)(4s-4c)(4s-4d)}$
= $\sqrt{4*4*4*4*(s-a)(s-b)(s-c)(s-d)}$  = $16*Area$
Thus, there is 1500% increase in the area.
Hence, option D is the correct answer.

Question 9: Consider a rectangle ABCD of area 90 units. The points P and Q trisect AB, and R bisects CD. The
diagonal AC intersects the line segments PR and QR at M and N respectively. What is the area of the quadrilateral PQNM?

a) > 9.5 and ≤ 10

b) > 10 and ≤ 10.5

c) > 10.5 and ≤ 11

d) > 11 and ≤ 11.5

e) > 11.5

9) Answer (D)

Solution:

Let us draw the figure according to the available information,

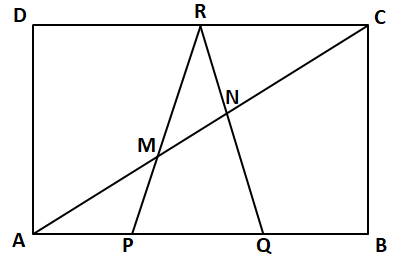
In $\triangle$ AMP and $\triangle$ CMR

$\angle$ MAP = $\angle$ MCR

$\angle$ AMP = $\angle$ CMR

Therefore, we can say that $\triangle$ AMP $\sim$ $\triangle$ CMR

Hence, we can say that $\dfrac{AP}{CR}=\dfrac{MP}{MR}$

$\Rightarrow$ $\dfrac{AB/3}{AB/2}=\dfrac{MP}{MR}$

$\Rightarrow$ $MR=\dfrac{3}{2}*MP$

Therefore, we can say that $\Rightarrow$ $MR=\dfrac{3}{5}*RP$   … (1)

Similarly, in $\triangle$ ANQ and $\triangle$ CNR

$\angle$ NAQ = $\angle$ NCR

$\angle$ ANQ = $\angle$ CNR

Therefore, we can say that $\triangle$ ANQ $\sim$ $\triangle$ CNR

Hence, we can say that $\dfrac{AQ}{CR}=\dfrac{NQ}{NR}$

$\Rightarrow$ $\dfrac{2AB/3}{AB/2}=\dfrac{NQ}{NR}$

$\Rightarrow$ $NR=\dfrac{3}{4}*NQ$

Therefore, we can say that $\Rightarrow$ $NR=\dfrac{3}{7}*RQ$  … (2)

In $\triangle$ RMN and $\triangle$ RPQ

$\dfrac{\text{Area of triangle RMN}}{\text{Area of triangle RPQ}} = \dfrac{0.5*RM*RN*sinMRN}{0.5*RP*RQ*sinPRQ}$

$\text{Area of triangle RMN}=\dfrac{3}{5}*\dfrac{3}{7}*\text{Area of triangle RPQ}$

We know that, Area of triangle RPQ = 1/6*Area of rectangle ABCD = 1/6*90 = 15 sq. units

$\Rightarrow$ $\text{Area of triangle RMN}=\dfrac{3}{5}*\dfrac{3}{7}*15$ = $\dfrac{27}{7}$ sq. units

Hence, the area of the quadrilateral PQNM = 15 – $\dfrac{27}{7}$ = $\dfrac{78}{7}=11\dfrac{1}{7}$ sq. units. Therefore, option D is the correct answer.

Question 10: In quadrilateral PQRS, PQ = 5 units, QR = 17 units, RS = 5 units, and PS = 9 units. The length of the diagonal QS can be:

a) > 10 and < 12

b) > 12 and < 14

c) > 14 and < 16

d) > 16 and < 18

e) cannot be determined

10) Answer (B)

Solution:

In a triangle , sum of two sides is greater than the third side and difference of two sides is less than third side.

In $\triangle$ PQS

=> $QS < 9 + 5$ => $QS < 14$ ——Eqn(I)

In $\triangle$ QRS

=> $QS > 17 – 5$ => $QS > 12$ ——Eqn(II)

From eqn(I) & (II)

=> $12 < QS < 14$

Question 11: ABCD is a quadrilateral such that AD = 9 cm, BC = 13 cm and ⎿DAB = ⎿BCD = 90°. P and Q are two points on AB and CD respectively, such that DQ : BP = 1 : 2 and DQ is an integer. How many values can DQ take, for which the maximum possible area of the quadrilateral PBQD is 150 sq.cm?

a) 14

b) 12

c) 10

d) 9

e) 8

11) Answer (D)

Solution:

Let $DQ = x$, => $BP = 2x$

Acc. to ques,

=> $ar (\triangle BPD) + ar (\triangle BQD) \leq ar (PBQD)$

=> $(\frac{1}{2} \times AD \times BP) + (\frac{1}{2} \times BC \times QD) \leq 150$

=> $(\frac{1}{2} \times 9 \times 2x) + (\frac{1}{2} \times 13 \times x) \leq 150$

=> $31x \leq 300$ => $x \leq \frac{300}{31}$

=> $x \leq 9.68$

Thus, for $x$ to be an integer and positive, 9 different values (1 to 9) are possible.

Question 12: 
AB is the diameter of the given circle, while points C and D lie on the circumference as shown. If AB is 15 cm, AC is 12 cm and BD is 9 cm, find the area of the quadrilateral ACBD.

a) 54sq. cm

b) 216sq. cm

c) 162sq. cm

d) None of these

12) Answer (D)

View Video Solution

Solution:

Since ACBD is cyclic quadrilateral with diagonals as AB = 15 ad CD.
So area = $\frac{1}{2} \times (AB) \times (CD)$                  eq.(1)
Triangle ACB and ABD is right angled triangle
Let’s say angle CBA = $\theta$
so $CD = 2 \times (9 sin\theta)$  (Where  $sin\theta$ = $\frac{12}{15}$)
CD = $\frac{72}{5}$
Putting values in eq. (1) , we will get area = 108 sq.cm.
Hence answer will be D)

Question 13: Let the consecutive vertices of a square S be A,B,C &D. Let E,F & G be the mid-points of the sides AB, BC & AD respectively of the square. Then the ratio of the area of the quadrilateral EFDG to that of the square S is nearest to

a) 1/2

b) 1/3

c) 1/4

d) 1/8

13) Answer (A)

View Video Solution

Solution:

Let the side of the square be 1 cm

So, area of triangle AGE = 1/2 * 1/2 * 1/2 = 1/8

Similarly, area of triangle EBF = 1/8

Area of triangle DFC = 1/2 * 1 * 1/2 = 1/4

Area of the square = 1*1 = 1

So, area of the quadrilateral = 1 – (1/8 + 1/8 + 1/4) = 1 – 1/2 = 1/2

Option a) is the correct answer.

Question 14: What is the area under the line GHI-JKL in the given quadrilateral OPQR, knowing that all the small spaces are squares of the same area?
I. Length ABCDEQ is greater than or equal to 60.
II. Area OPQR is less than or equal to 1512.

a) The question can be answered with the help of statement I alone.

b) The question can be answered with the help of statement II, alone.

c) Both, statement I and statement II are needed to answer the question

d) The question cannot be answered even with the help of both the statements.

14) Answer (C)

View Video Solution

Solution:

Let the side of the smallest square be x.

According to statement 1,$10x\geqslant 60$

$x\geqslant 6$

According to statement 2, $7x*6x\leq 1512$

$x\leq 6$

From both the statements x = 6 and the answer can be determined.

Instructions

Directions for the next two questions: Answer the questions based on the following diagram

In the following diagram, $\angle{ABC}$ = 90° = $\angle{DCH}$ = $\angle{DOE}$ = $\angle{EHK}$ = $\angle{FKL}$ = $\angle{GLM}$ = $\angle{LMN}$

AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL = 2LM = MN

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_8_1.png”/>

Question 15: What is the ratio of the areas of the two quadrilaterals ABCD to DEFG?

a) 1 : 2

b) 2 : 1

c) 12 : 7

d) None of these

15) Answer (C)

View Video Solution

Solution:

Area of ABCD = Area of triangle + Area of rectangle = Let AB = x. So, area = $3/2 * x^2 / 2 = 3/4 * x^2$
Area of ODE = $\frac{1}{2}* \frac{x}{2}*\frac{x}{2}$=$x^2/8$
Area of OEFI = $ \frac{x}{2}*\frac{x}{2}$=$x^2/4$
Area of FGI = $x^2/16$
Total area of DEFG = $7x^2/16$
Required ratio = 12:7

Download SSC Preparation App

Enroll to 15 SSC MTS 2022 Mocks At Just Rs. 149