In $$\triangle ABC$$, $$AB =AC= 12$$ cm and $$D$$ is a point on side $$BC$$ such that $$AD= 8$$ cm. If $$AD$$ is extended to a point $$E$$ such that $$\angle ACB = \angle AEB$$, then the length, in cm, of $$AE$$ is

Based on the information provided, we can construct the following diagram;

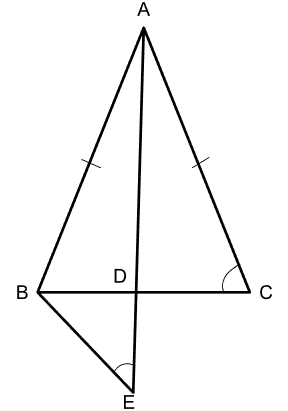
We have $$AB = AC = 12$$ cm, and $$AD = 8$$ cm.

Without loss of generalisation, we take $$AD$$ as an altitude of $$\triangle ABC$$. Therefore, in $$\triangle ACD$$, $$AC^2 = AD^2 + CD^2$$. We get $$AC^2 - AD^2 = CD^2$$, therefore, $$CD^2 = 12^2 - 8^2 = 80$$, or $$CD = \sqrt{80}$$.

Also, $$BD = CD$$, since $$AD$$ will also be the new median, being the altitude of the isosceles triangle. And $$BD = \sqrt{80}$$

In right-angled triangle $$\triangle ACD$$, $$\tan C = \dfrac{AD}{CD} = \dfrac{8}{\sqrt{80}}$$

In right-angled triangle $$\triangle BDE$$, $$\tan E = \dfrac{BD}{DE} = \dfrac{\sqrt{80}}{DE}$$

Since $$\angle C = \angle E$$, we have $$\tan C = \tan E$$, therefore,

$$\dfrac{8}{\sqrt{80}} = \dfrac{\sqrt{80}}{DE}$$

$$\Rightarrow DE = \dfrac{80}{8} = 10$$

Since $$AE = AD+DE$$, we get $$AE = 8+10= 18$$ cm. 

The correct answer is option C.